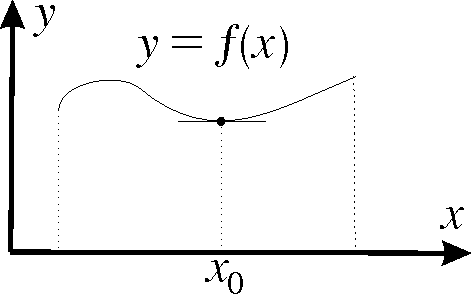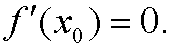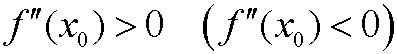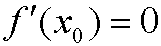1. Functions - extreme points.
Consider a real valued function
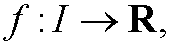where I is an open interval in R. We say that f has a local minimum in the point x0 in I if
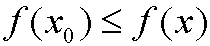for all x in some neighborhood to x0 in I.
A local maximum is defined in a corresponding way.
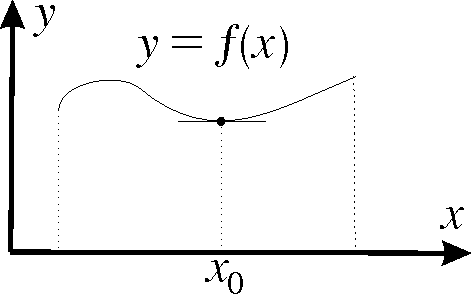It is well known that if f is differentiable, a necessary condition for x0 to be an extreme point (local maximum or minimum) is
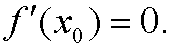Note that the conversion in general does not hold, but if f also fulfills
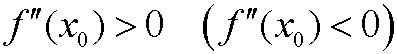then f has a local minimum (maximum) in x0 .
Remark: A point x0 that fulfills
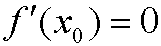is called a stationary point of f.
