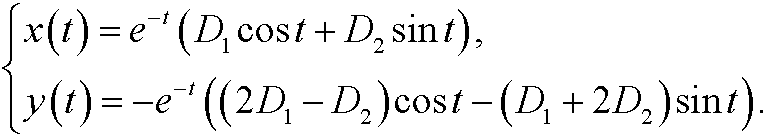8. The general solution of a linear system.

Consider the linear dynamical system

 

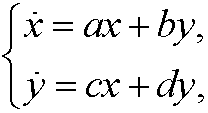
that is

 

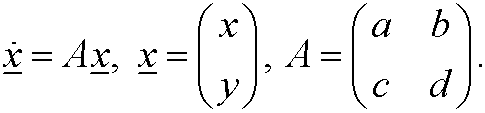
We look for solutions on the form

 

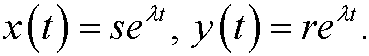
If we instert these to the system we get

 

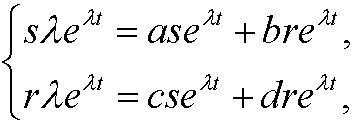
that is

 

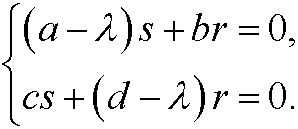
This equation system has nontrivial solutions if and only if

 

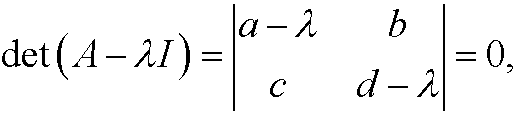
that is, if and only if

 

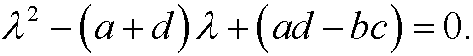
This is the characteristic equation of the system and the solutions  its eigenvalues. If we now for each eigenvalues   solve the equation system

 

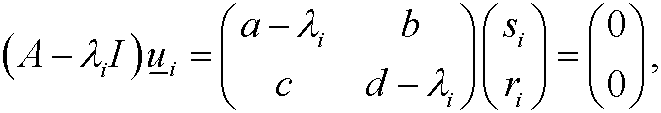
we obtain the eigenvectors

 

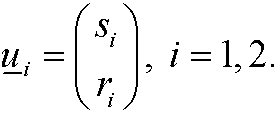
Then we have the general solution of our original dynamical system as

 

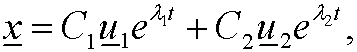
that is

 

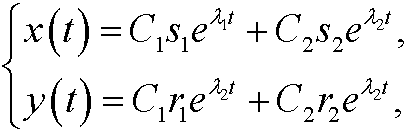
where C₁ and C₂ are arbitrary constants.

Example 8: Assume that the matrix A is

 

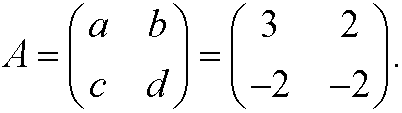
This matrix has characteristic equation

 

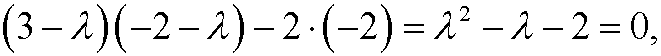
with the eigenvalues 

 

and corresponding eigenvectors

 

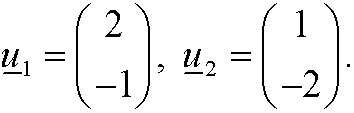
This means that the general solution of the corresponding dynamical system is

 

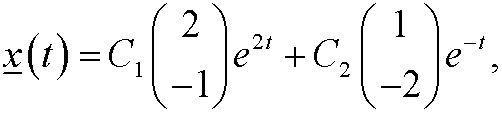
that is

 

Example 9: Solve the system

 

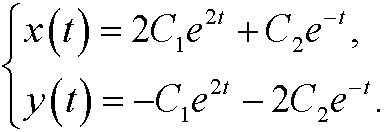
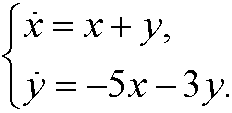
Solution: We consider the matrix

 

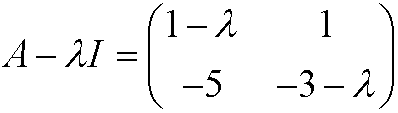
and its characteristic equation

 

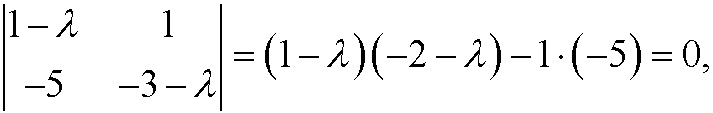
that is

 

The eigenvalues thus are

 

with corresponding eigenvectors

 

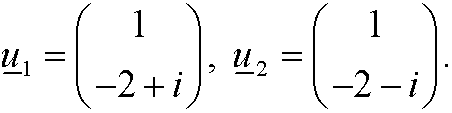
This means that the dynamical system has the general solution

 

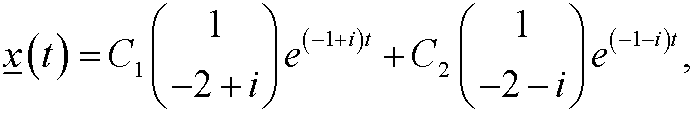
that is

 

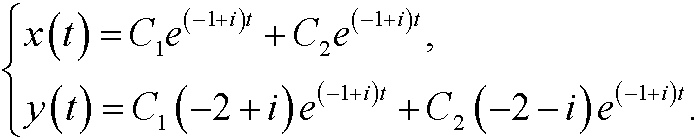
These are all complex solutions. We are actually only interested in the realsolutions. With help of Euler’s formula we get

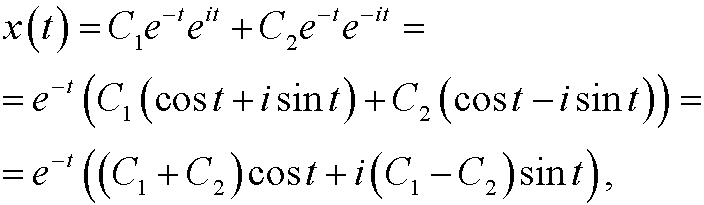
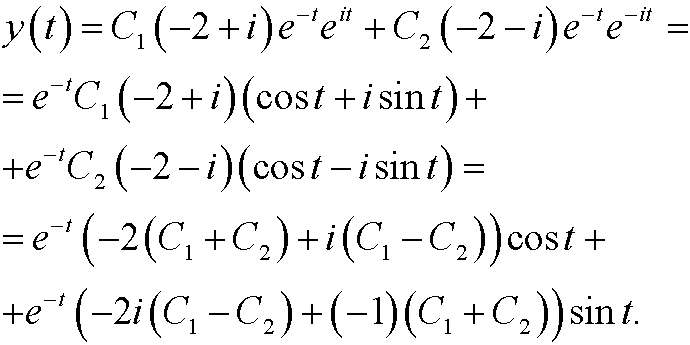
If we now pick arbitrary real constants D₁ and D₂ and put

 

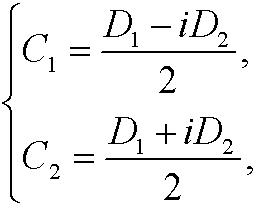
we get the general real solution