1.1) A physical phenomenon is described by the quantities pressure P, length l, mass m, time t och density 
. If there is a physical law
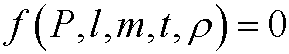
relating these quantities, show that there is an equivalent physical law on the form
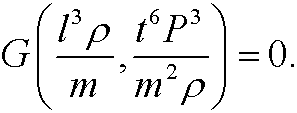
1.2) Let
be a given continuous function. If M=max|u(t)| then u can be scaled with M to the dimensionless variable U=u/M. As time scale we can use N=M/max|u'(t)|, the ratio between the maximal value of the function and its maximal slope. Find M and N for the the following functions:
a)
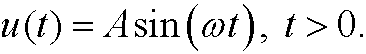
b)
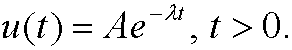
c)
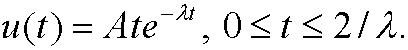
1.3) Consider the function
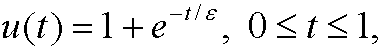
where 
is a small number. Use exercise 1.2 to find a time scale. Is this time scale suitable for all the interval [0,1]? (Draw a graph of u(t) when 
). Explain why two different time scales might be needed for a process described by u(t).
1.4) A pendulum that is l long and has mass m swings around its point of fixing. We denote the angle between the vertical line and the pendulum with 
. This means that 
is 0 when the pendulum is directed straight down.
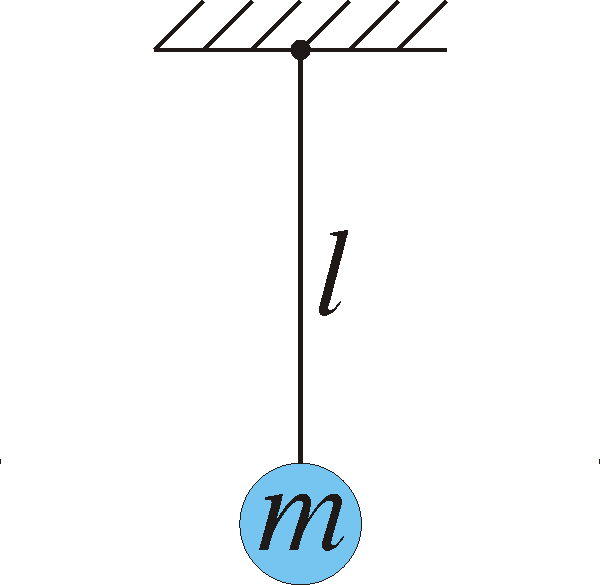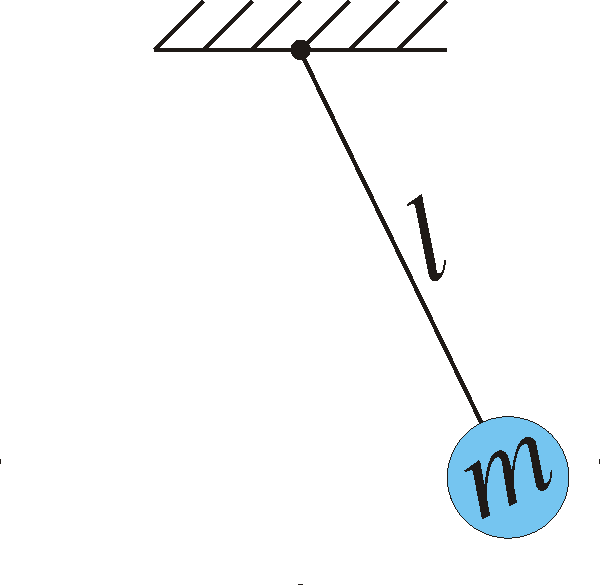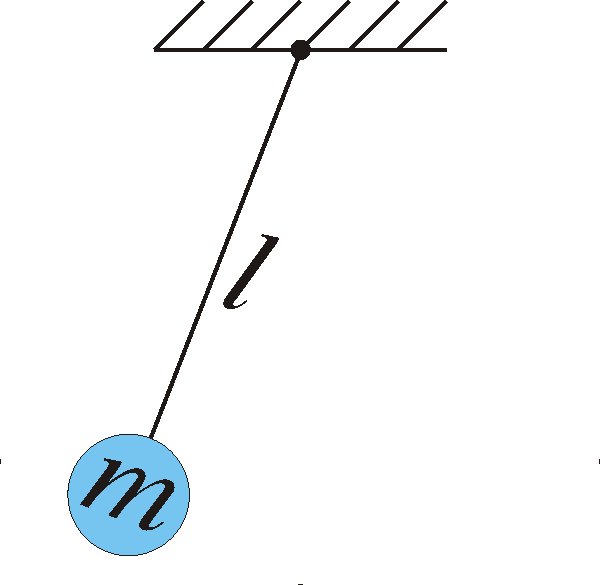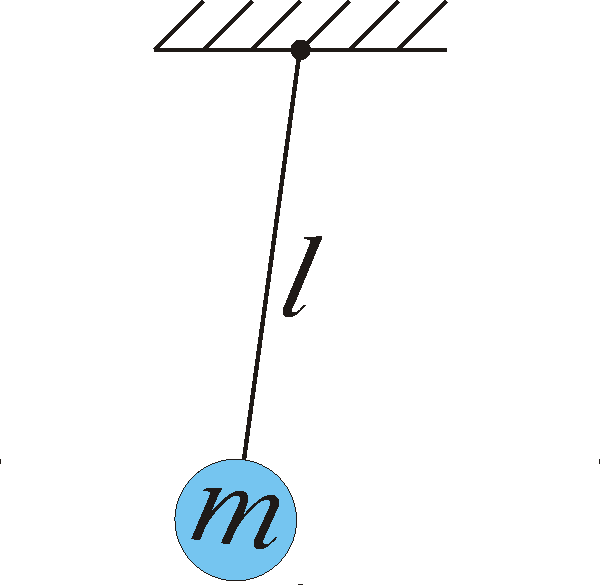
Use Newton’s second law to derive its equation of motion (note that the acceleration of the mass is d2s/dt2 where 
is the length of the circular arc that the mass travels along, that the force is -mg vertically downward and that it is only the tangential component of the force that affects the motion.) The mequation of motion will then become
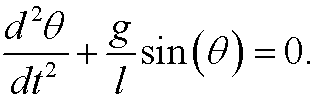
If the mass is released from a small angle 
at time t=0, formulate a dimensionless initial value problem that describes the motion.
1.5) Present and discuss Malthus’ logistic model for population dynamics. Introduce dimensionless variables and make a suitable scaling. Solve the scaled equation and find an attractor to the original equation. What does this attractor mean in practice?