We define fn(x) for a given function f(x) and a given starting value x0 by
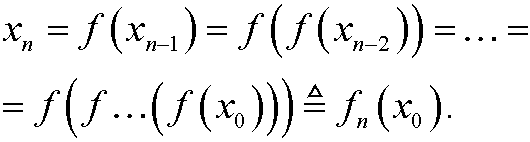
By the chain rule we then have that
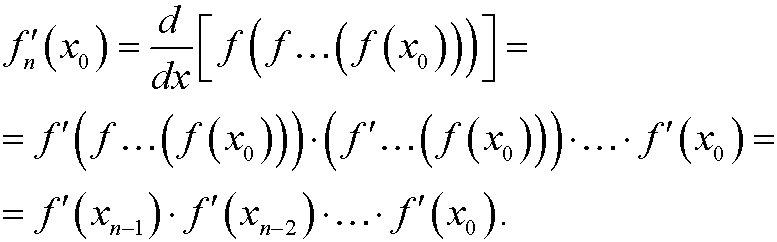
By taking logarithms and dividing by n on both sides we get
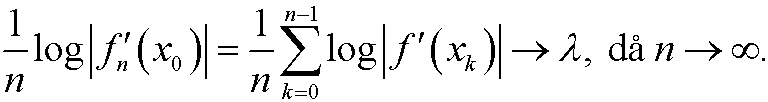
This convergence can be proved by using a particular mathematical technique. The limit ![]() is called the Lyapunov exponent of the dynamical system.
is called the Lyapunov exponent of the dynamical system.
Now suppose that we have two (close) starting values x0 and y0. By using the mean value theorem we see that
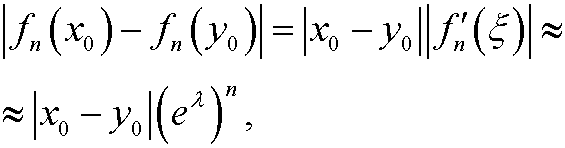
since

and
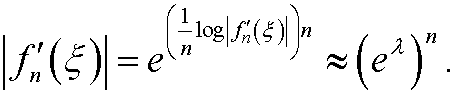
The conclusion is that
a) if ![]() we have that
we have that
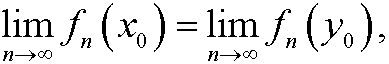
that is, the system is not sensitive to the starting value.
b) if ![]() then
then
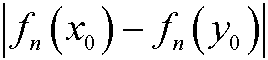
diverges to infinity with exponential growth.