5. Comparison with the exact solution.

Again consider the differential equation

 

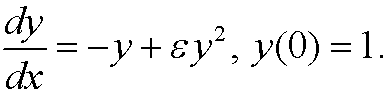
As we said before, the exact solution is then

 

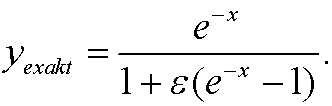
By using maclaurin expansion we know that

 

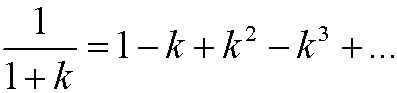
for small values of k. If we insert

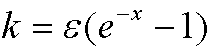
we get

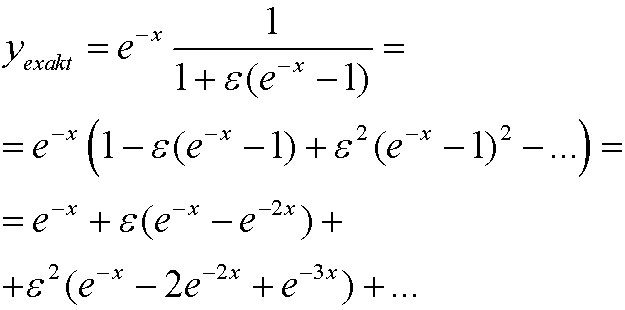
Now compare with the approximate solution from last part

 

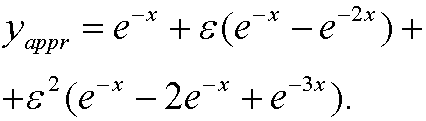
We see that the error E in the approximation thus is

 

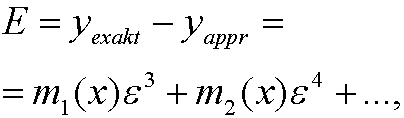
for some dunctions m₁(x), m₂(x),… (that we can compute!). We say that the error E is of order  and write E=O( ), where O stands for big ordo.