Let
where V is some set, be a continuous function. If x0 is a given starting point, we define the orbit: x0, x1, x2,… of the system by
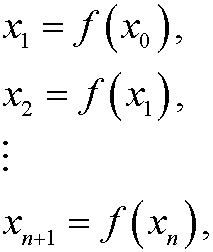
that is, xn is the state of the dynamical system at time step n.
Main problem: What can we say about xn for large values of n?
We have chaos if small changes in x0 implies large (or unpredictable) changes in xn.
An attractor is a stable state for the dynamical system for large values of n.
Example 1: Verhulst’s population model. Let
be a parameter and define
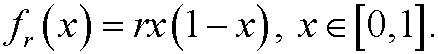
This is a useful description of the growth of a population. The orbit x0, x1, x2,… is obtained in the following way: Assume that we have a starting value x0 year 0. Then compute
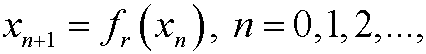
where xn is the population year n.
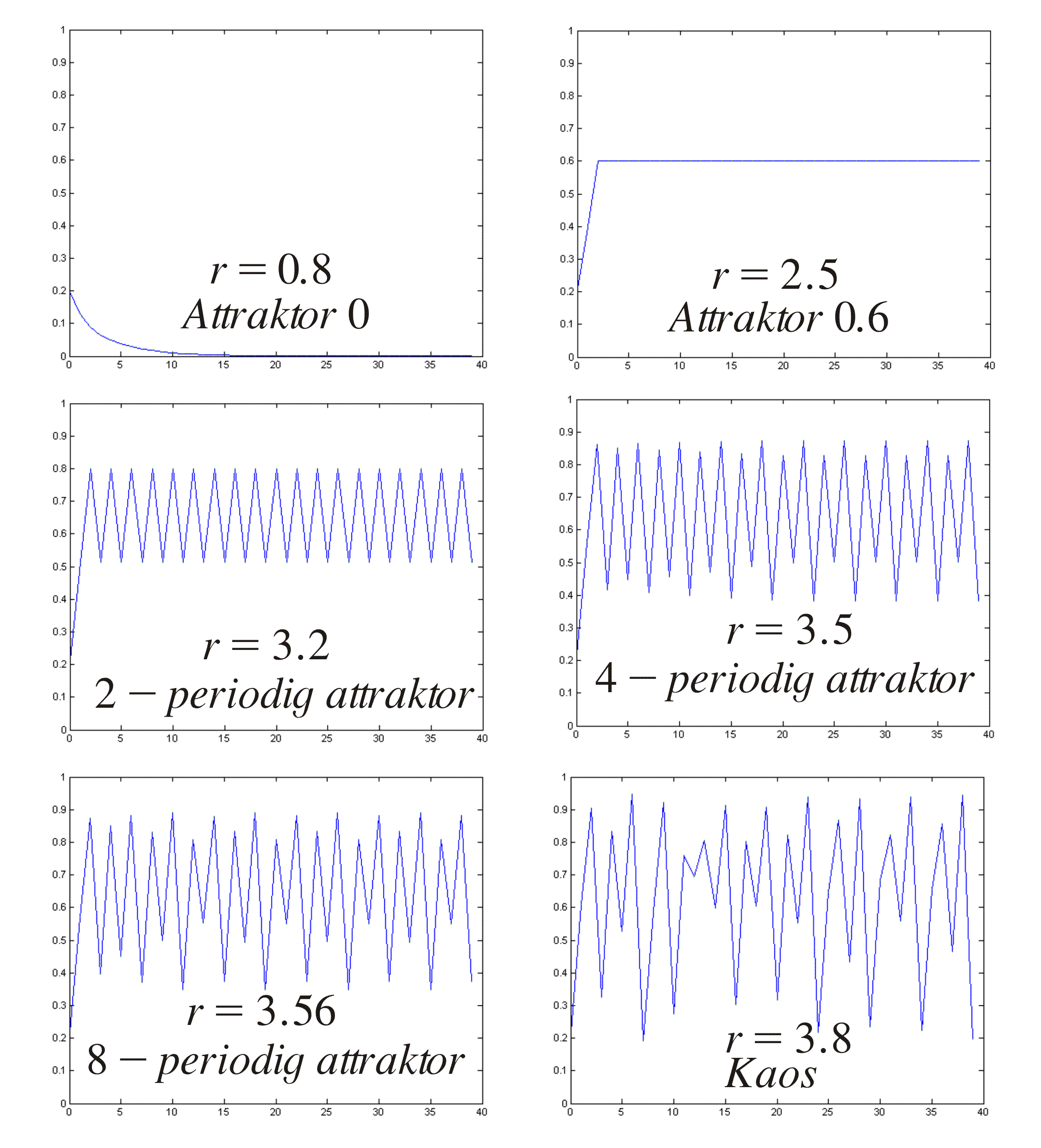
As we see above, different values of r give very different behavior of the behavior of the orbit (try yourself with a calculator).
We see that the orbit converges to an attractor in the cases where we do not have chaos. Describe the attractor in the different cases!
It can be shown that the following holds: There is a sequence of parameters r1,r2,r3,… such that
* if 0<r<r1=1, the sequence {xn} converges to the attractor 0.
* if 1=r1<r<r2=3, the sequence {xn} converges to a (constant) attractor 1-1/r.
* if 3=r2<r<r3 the sequence {xn} converges to a periodic state with two different values.
* if r3<r<r4 the sequence {xn} converges to a periodic state with four different values.
.
.
* if rk<r<rk+1 the sequence {xn} converges to a periodic state with 2k-1different values.
* if r>r* we have chaos. The long term behavior is not periodic and the behavior of the orbit extremely depends on the starting value x0. This is not the case for r<r*. The value r*=3.569945672…
For more information about this behavior, see this page. The behavior above r2=3 is called period doubling and can be illustrated in a so called bifurcation diagram.
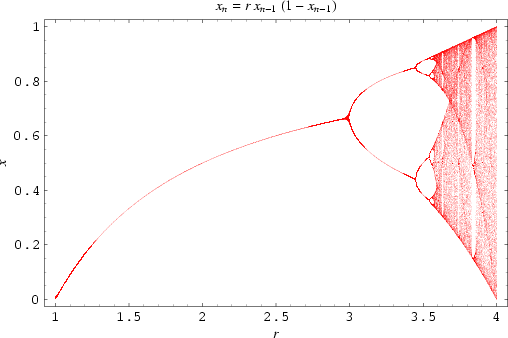
We can now define Feigenbaum‘s constant, as the limit of the quotient
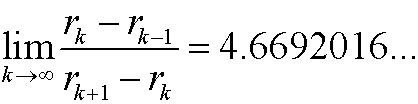
The interesting about this constant is that it also appears for several other functions fr(x) and thus also other values of rk!