14. Matching.

 

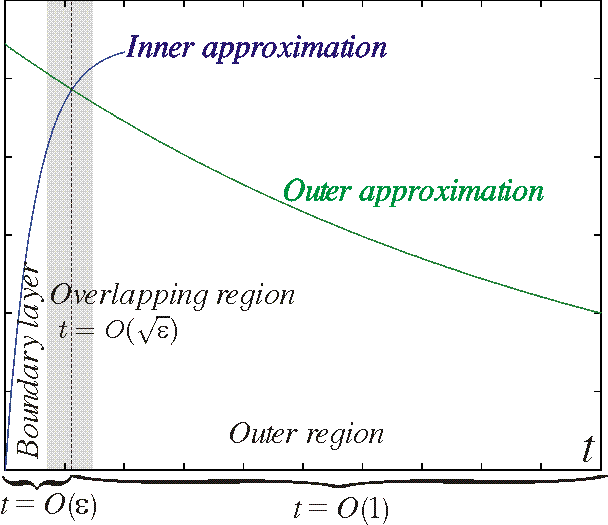
In the overlapping region we let

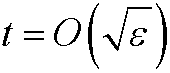
and introduce the intermediate variable

 

This is a time scale that is “between” de inner

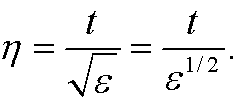
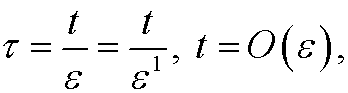
and outer

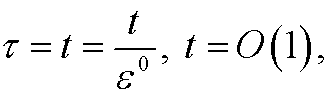
time scales. To be able to match the approximations we require that the outer and inner approximations (written with respect to the intermediate variable) must agree in the limit

 

that is

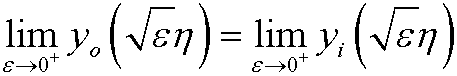
for a fix (positive) value of . in our case this means that

 

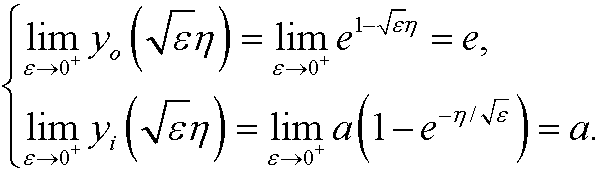
VWe realize that a=e and that our inner approximation therefore must be

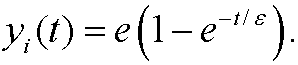
Finally, we want to find a solution that is valid in all the interval [0,1]. We therefore construct y_u from the inner and outer approximations minus their common limit e (since it otherwise would have been counted twice) in the overlapping region

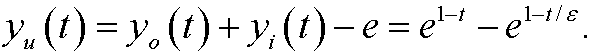
When t is in the outer region the second term is small and y_u is thus approximately

which is exactly the outer approximation. When t is in the boundary layer the first term is close to e and y_u is thus approximately

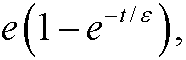
which is exactly the inner approximation. In the overlapping region both the inner and outer approximations are approximately equal to e, which makes the sum of  y_i and y_o close to 2e there, that is, twice as much as it should be. That is why we have to subtract the common limit from the sum. If we insert y_u in the original differental equation we see that

dthat is, y_u fulfills the equation exactly on the interval (0,1). If we investigate the boundary conditions we see that

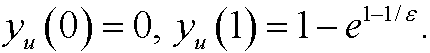
The left condition is exactly fulfilled and the right is fulfilled up to

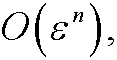
´for any n>0 , since

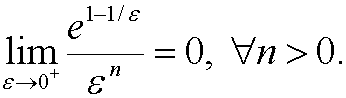
We thus see that y_u is a unitly good approximation on [0,1].