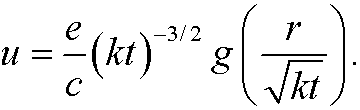We consider a typical heat conduction problem. At time t=0 we let an amount of heat e concentrated in a point in space diffuse outward in a region with original temperature zero.

If r denotes the radial distance from the source and t is the time, then the problem consists of determine the temperature u as a function of r and t. We easily realize that the temperature u depends on t, r and e. It is also reasonable that it depends on the heat capacity c of the region as well as the speed with which the heat diffuses outward (the heat diffusivity k). We therefore assume a physical law on the form
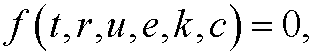
relating the fundamental quantities t, r, u, e, k, c. These quantities have the dimensions
| Symbol: |
Quantity: |
Dimension: |
| t |
time |
T |
| r |
length |
L |
| u |
temperature |
|
| e |
energy |
E |
| k |
heat diffusivity |
L2/T |
| c |
heat capacity |
The dimension matrix A then becomes
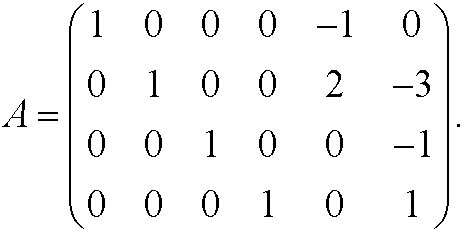
We thus have m=6 (number of physical quantities), n=4 (number of fundamental dimensions) and r=4 (rank of the dimension matrix). This implies that we can construct m-r=6-2=2 dimensionless quantities. We therefore look for two linearly independent solutions of the system
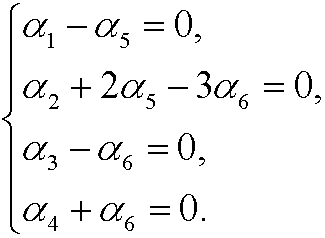
If we let
we get
that is
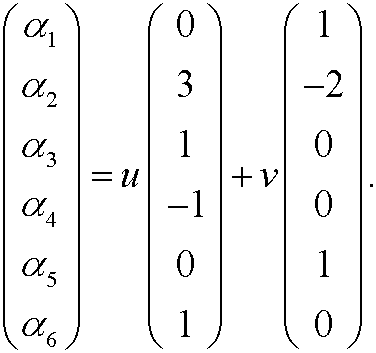
If we choose v=-1/2 and u=0, we get one solution
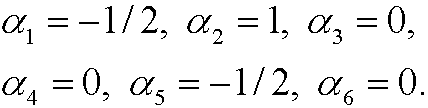
If we choose u=1 and v=3/2, we get another (linearly independent) solution
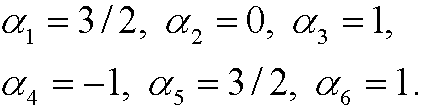
These two solutions give the two dimensionless variables
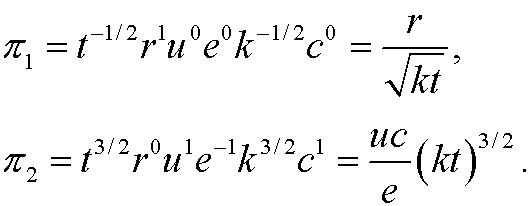
According to the Pi-theorem we then conclude that there is an equivalent relation
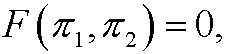
that is
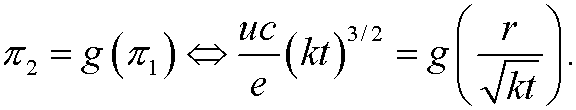
If we finally solve for u, we get