If we get the remainder r=0 after division of a by a number b, we say that b divides a (or that a is divisible by b). The number b is then called a divisor in a. We write b|a. We have for example that
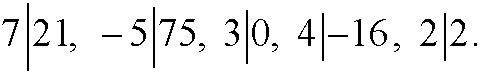
If an integer a bigger than 1 do not have other divisors than ±1 and ±a, it is called a prime number. The first prime numbers are
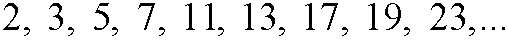
We directly realize that 2 is the only even prime number, since all other even numbers have 2 as divisor. An integer which is not prime is called a composite number. A composite number can always be factorized by prime factors, a fact that is guaranteed by the following theorem:
Theorem: (Fundamental theorem of arithmetic) Every integer larger than one can uniquely be written as a product of primes.
By the fundamental theorem we can draw the conclusion that there is infinitely many primes. Indeed, suppose that the number of primes was finite, say n primes. Now multiply all these primes pi and add 1. The number T we have obtained can not be divisible by any of those primes we started with, since they would all give the rest 1 if we would divide T by them. Hence we must have obtained a new prime or a product of new primes. Our reasoning leads to a contradiction. Thus must our assumption of finitely many primes be false. This was proved already about 300 BC by Euclid.
If a number d divides bothe the number m and the number n, we call d acommon divisor. For instance, 6 is a common divisor for 24 and 36. Often, one wants to find the largest common divisor gcd(n,m) for two numbers nand m. For the numbers 24 and 36, we have
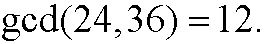
In order to find the largest common divisor, we can prime factorize both numbers and examine which prime factors that appear in both numbers, that is, the largest common divisor will be (the product of the elements in) the intersection of the sets of prime factors for both numbers. However, the procedure of prime factorizing numbers is very tedious. Luckily, there is a very effective algorithm (invented by Euclid) to find the largest common divisor gcd(m,n). Start by dividing the larger number m with the smaller n. This gives a remainder r1. Then divide the smaller number n with the obtained remainder r1. This gives anew remainder r2. Now divide the remainder r1 with the remainder r2. This gives yet another remainder r3. Repeat the procedure until the remainder becomes zero. The last non-zero remainder is equal to the largest common divisor.
Example 1: Find gcd(7854,4746).
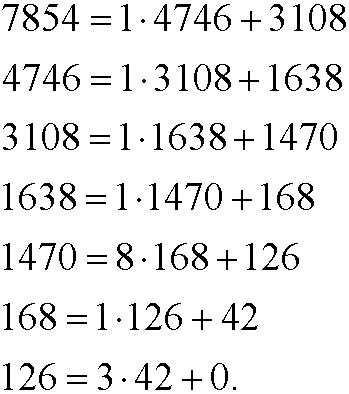
We thus have gcd(7854,4746)=42. The calculation above can be written gcd(7854,4746) = gcd(4746,3108) = gcd(3108,1638) = gcd(1638,1470) = gcd(1470,168) = gcd(168,126) = gcd(126,42) = 42, where the final step is obvious. To prove that the algorithm works we must show that gcd(m,n) = gcd(n,r), where m=qn+r. If d1 is a common divisor to m and n, we can write m=m1d1 and n=n1d1. Then r = m-qn = m1d1–qn1d1 = (m1-qn1)d1 also has d1 as divisor. If instead d2 is a common divisor to n and r, we can write n=n2d2 and r=r2d2. Then m = qn+r = qn2d2+r2d2 = (qn2+r2)d2 also has d2 as divisor. That is, all common divisors to m and n are common divisors to n and r and vice versa. Then the numbers must have the same common divisors and of course also the same largest divisor.
Euclid’s algorithm can be extended such that we can write gcd(n,m) as a linear combination of n and m. We demonstrate the procedure with the same example as above, but backwards by successively replace the obtained remainders.
Example 2:
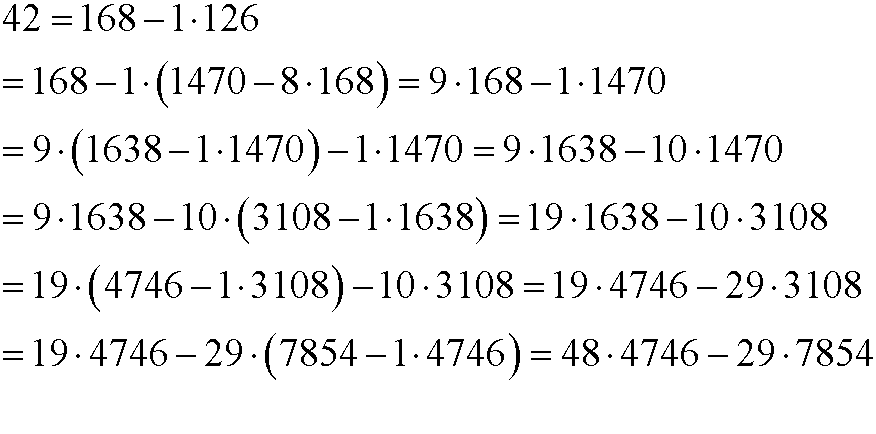
We can thus write
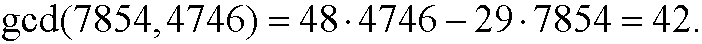
Another often sought after property is the least common multiple lcm(m,n) between two numbers m and n. The least common multiple is (the product of the elements in) the union of the sets of prime factors for both numbers. The union of two sets is obtained by writing down the element from both sets and removing those from the intersection of the sets, since those elements have been counted twice. The intersection was the greatest common divisor, thus we have the formula
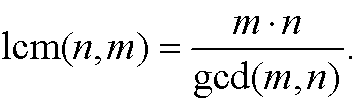
With help of the least common multiple, we can find infinitely many linear combinations of gcd(n,m). We demonstrate this in the example below.
Example 3: We have that
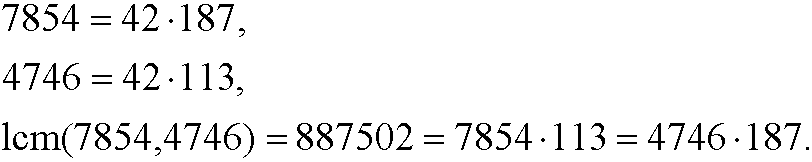
This implies that
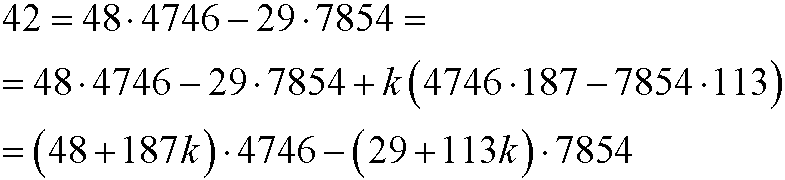
We thus have a linear combination for every choice of the integer k.