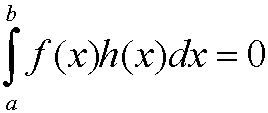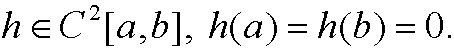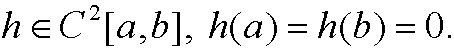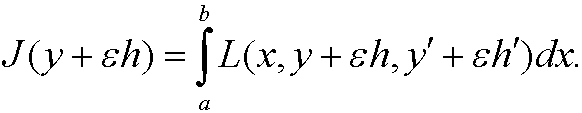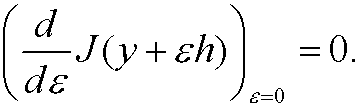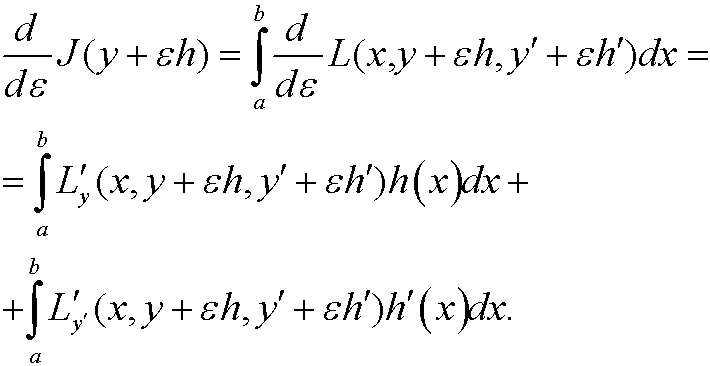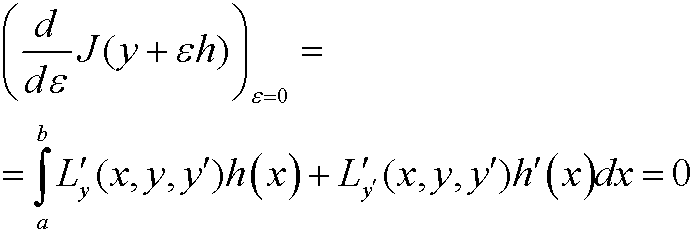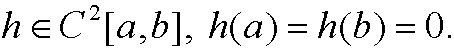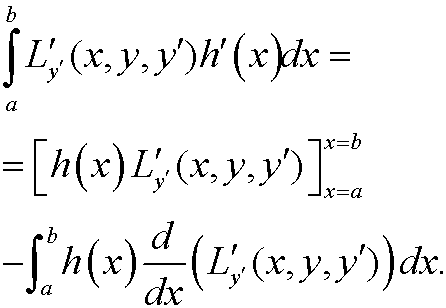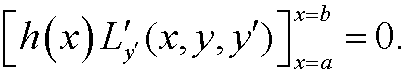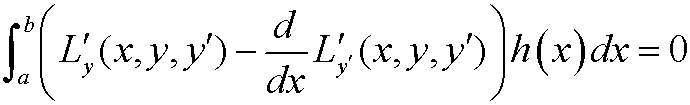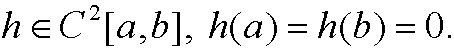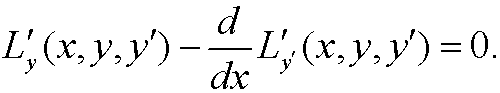8. Proof of theorem 1.

Lemma: Let f be a function in C[a,b] and assume that

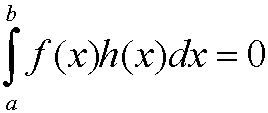for every

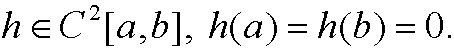Then

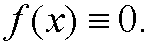Proof of theorem 1: Let y be an extremal and let

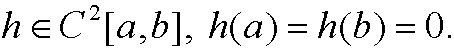Then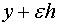

is an admissible and competing function for

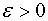. Consider the functional

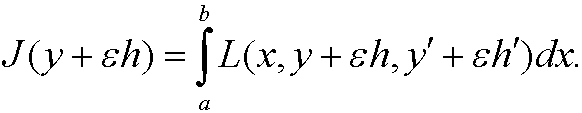Since y is an extremal we must have

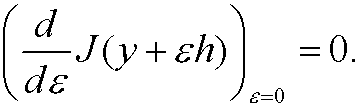If we move the derivative inside the integral we get

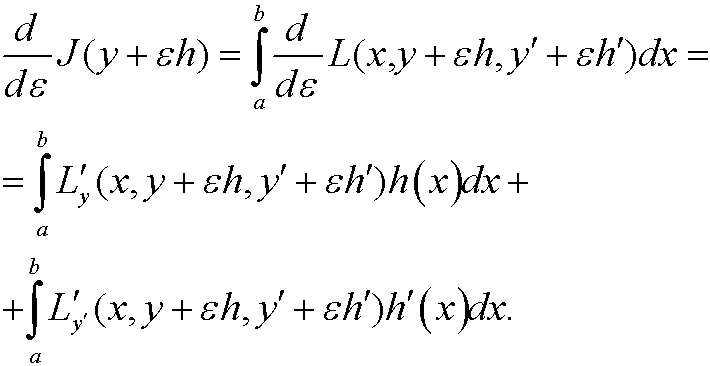This means that

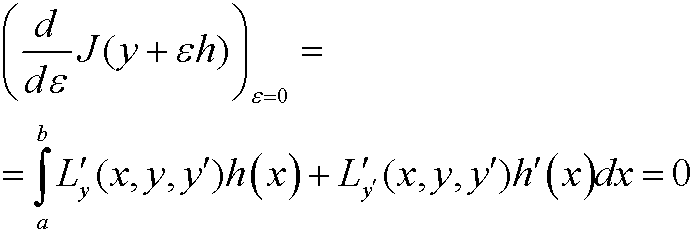for all

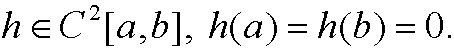We integrate the second term by parts and get

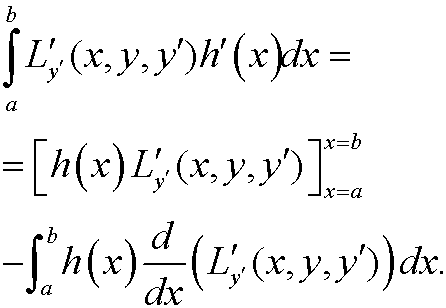
<>Since

this implies that

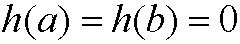
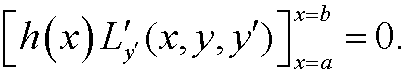We thus have

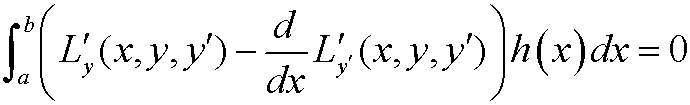for all

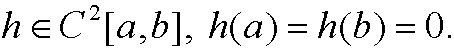If we finally use the lemma above we can conclude that

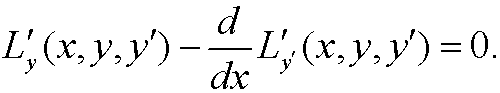The proof is complete.