We will here formulate some simple models for poplation dynamics in a closed ecosystem. Such models play an important role when it comes to understanding the factors that contributes to increase in population. Let P=P(t) denote the size of the population at time t and P0denote the size of the population at time t=0.
The most simple model is known as Malthus’ model and it says that the increase in population is proportional to the size of the population, that is
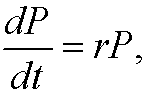
where r is a constant speed of growth. This model predicts that the population will increase exponentially, that is
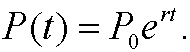
This would lead to a population explosion. Is this model reasonable? As the population grows, the amount of food, living space and natural resources will limit the growth. We should therefore correct Malthus’ model with a limiting term. The growth not only depend on the size of the population but also on how far it is from its upper limit. We must correct with a term that makes the growth decrease and becomes zero when we reach this upper limit K. We have thus reached the logistic model (also known as Verhulst’s population model)
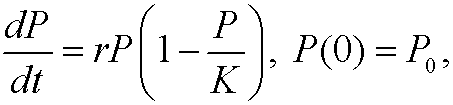
where K is a constant that can be interpreted as the largest amount of individuals that an ecosystem kan nourish (the so called carrying capacity).
Now we scale this model. We introduce a dimensionless time
and a dimensionless population
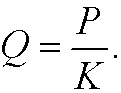
We can now write the logistic equation in these dimensionless variables
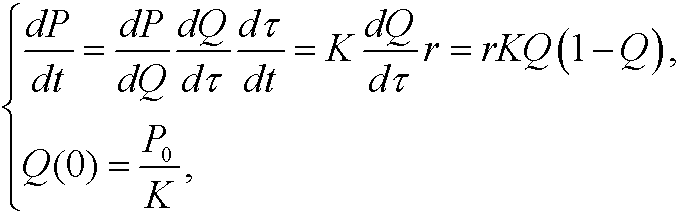
that is
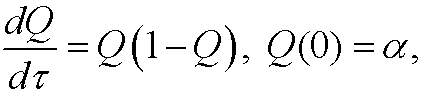
where
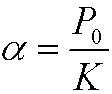
is dimensionless. This differential equation can for instance be solved by separation of variables
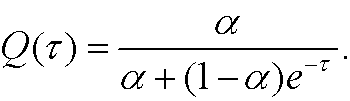
We easily realize that
that is
<>The constant solution P=K is called attractor and has the property that independent of the size of the initial population, the size of the population will tend to K as the time goes to infinity. Attractors and related phenomena of dynamical systems will be examined in chapter IX.