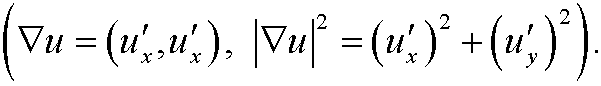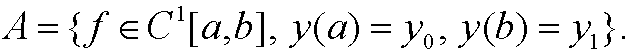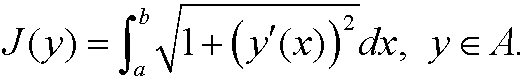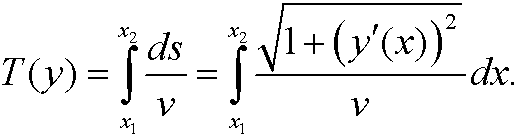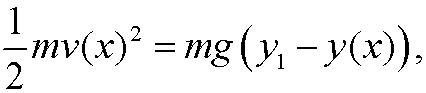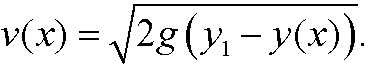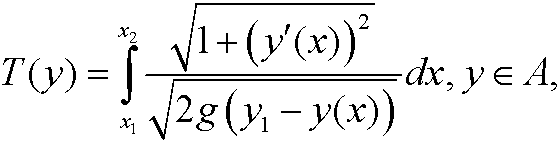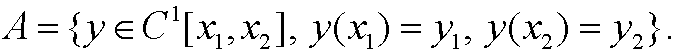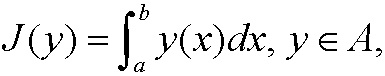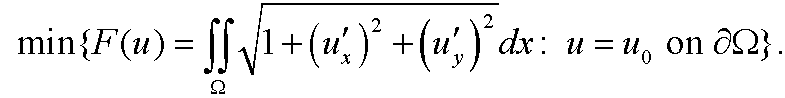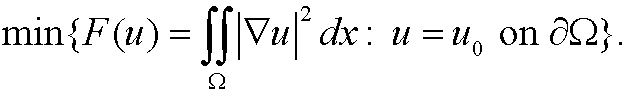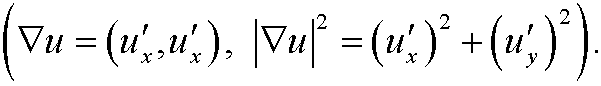4. Some examples of variational problems.
Example 4: Let A be the set
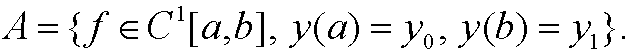 Find minimum to the functional J(y) when
Find minimum to the functional J(y) when
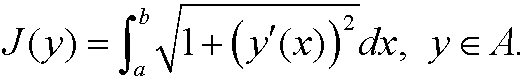 Remark: This functional describes the curve length between the points (a,y0) and (b,y1) (see the figure below).
Remark: This functional describes the curve length between the points (a,y0) and (b,y1) (see the figure below).
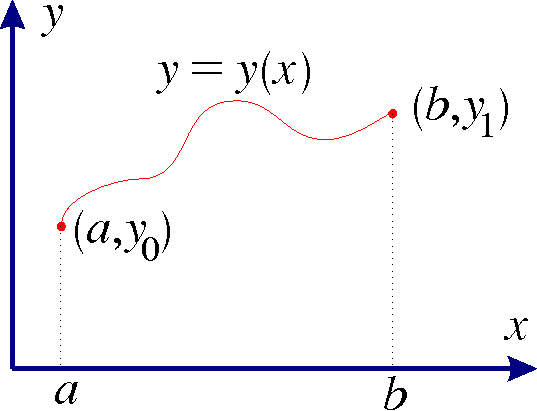 Example 5 (The Brachistochrone problem), from Greek brachistos(shortest) and chronos (time)): A particle with mass m starts from rest and glides without friction under the influence of gravity from the point (x1,y1)to the point (x2,y2) along the curve y=y(x) in the xy-plane. What curve gives the shortest time of descent? (Bernoulli 1696).
Example 5 (The Brachistochrone problem), from Greek brachistos(shortest) and chronos (time)): A particle with mass m starts from rest and glides without friction under the influence of gravity from the point (x1,y1)to the point (x2,y2) along the curve y=y(x) in the xy-plane. What curve gives the shortest time of descent? (Bernoulli 1696).
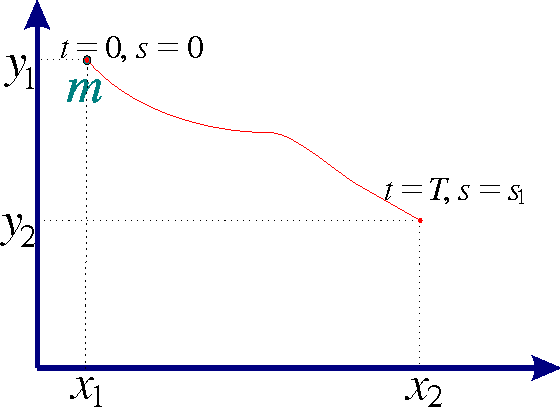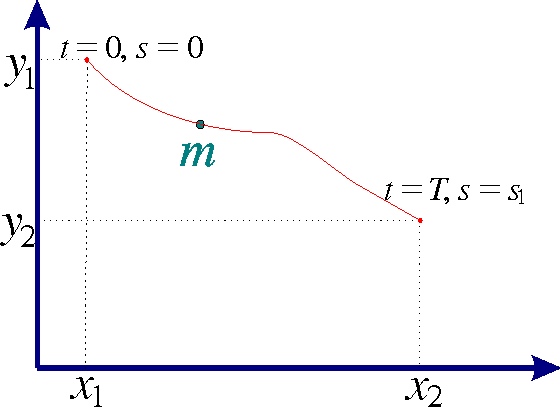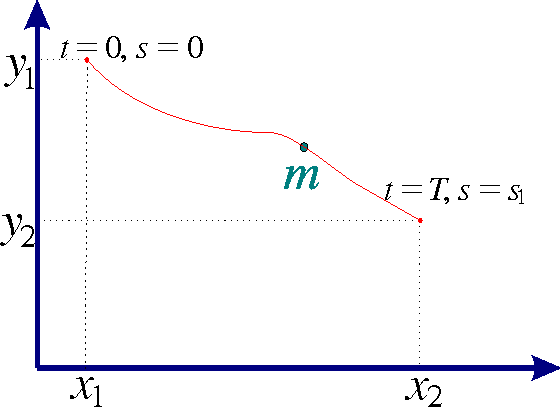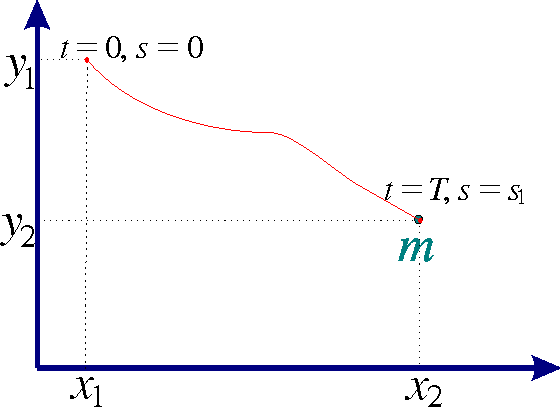 Since the speed along the curve is v=ds/dt, we have for the total time of descent that
Since the speed along the curve is v=ds/dt, we have for the total time of descent that
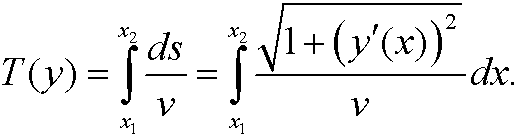 To compute v as function of the coordinates we use that a decrease of potential energy is followed by an equally large increase of kinetic energy assuming that we do not have any friction. If the acceleration of gravity is g, this implies that
To compute v as function of the coordinates we use that a decrease of potential energy is followed by an equally large increase of kinetic energy assuming that we do not have any friction. If the acceleration of gravity is g, this implies that
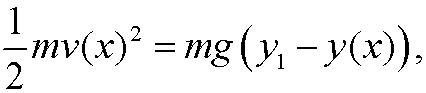 that is, the speedv(x) is given by
that is, the speedv(x) is given by
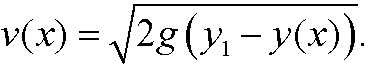 This leads to the variational problem of minimizing
This leads to the variational problem of minimizing
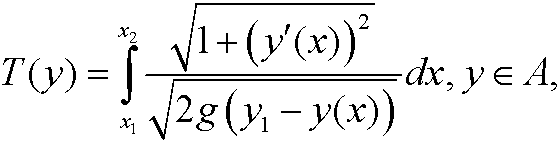 when
when
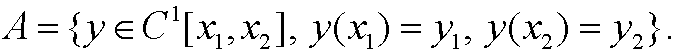 Example 6: Minimize the functional
Example 6: Minimize the functional
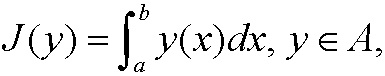 when
when
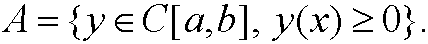 What is the interpretation of this problem and what is the solution?
Example 7: Let A be an arbitrary function space on [a,b]. Then
What is the interpretation of this problem and what is the solution?
Example 7: Let A be an arbitrary function space on [a,b]. Then
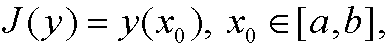 is also a functional.
Example 8 (the soap film problem, Plateau’s problem): Find
is also a functional.
Example 8 (the soap film problem, Plateau’s problem): Find
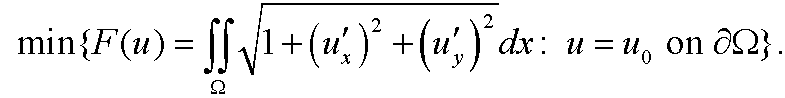 Remark: This functional describes the area of a surface that is spanned by the curve u0 on the boundary to
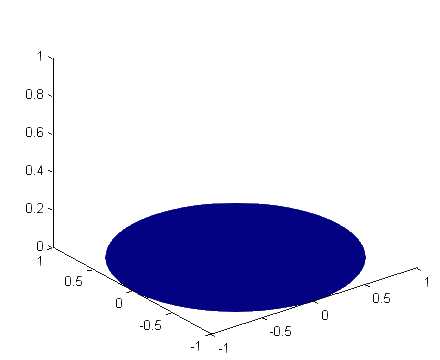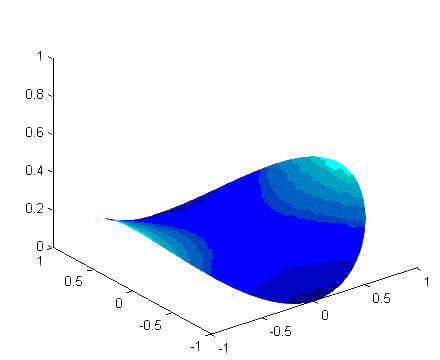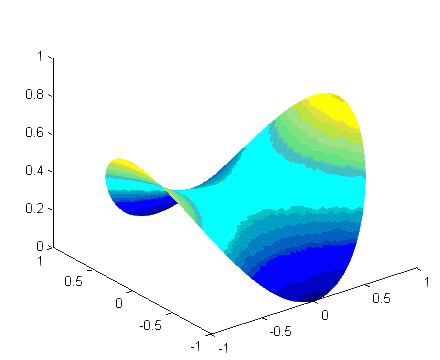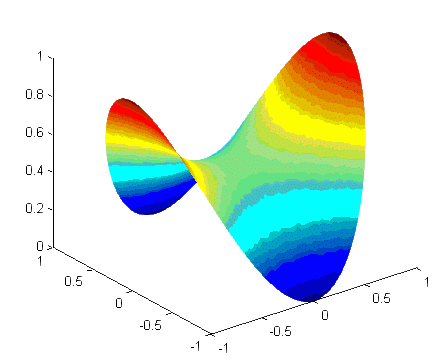
Remark: This functional describes the area of a surface that is spanned by the curve u0 on the boundary to  . The soap film we get by dipping a shaped wire in soap solution will fulfill the above variational problem. The figure below shows how a soap film on an elastic ring will change as the ring is stretched to a parabolic shape (in the x-direction).
. The soap film we get by dipping a shaped wire in soap solution will fulfill the above variational problem. The figure below shows how a soap film on an elastic ring will change as the ring is stretched to a parabolic shape (in the x-direction).
 Example 9 (Dirichlet’s integral, Principle of least work): Find
Example 9 (Dirichlet’s integral, Principle of least work): Find
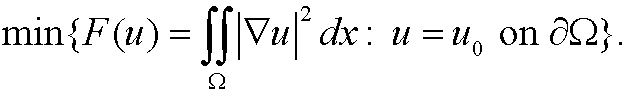 Remark:
Remark: