Exempel 1: (Harmonisk oscillator.) Consider a mass m suspended in a spring with spring constant k>0. We release the mass from a starting point at time 0 and let it swing oscillate around an equilibrium point.
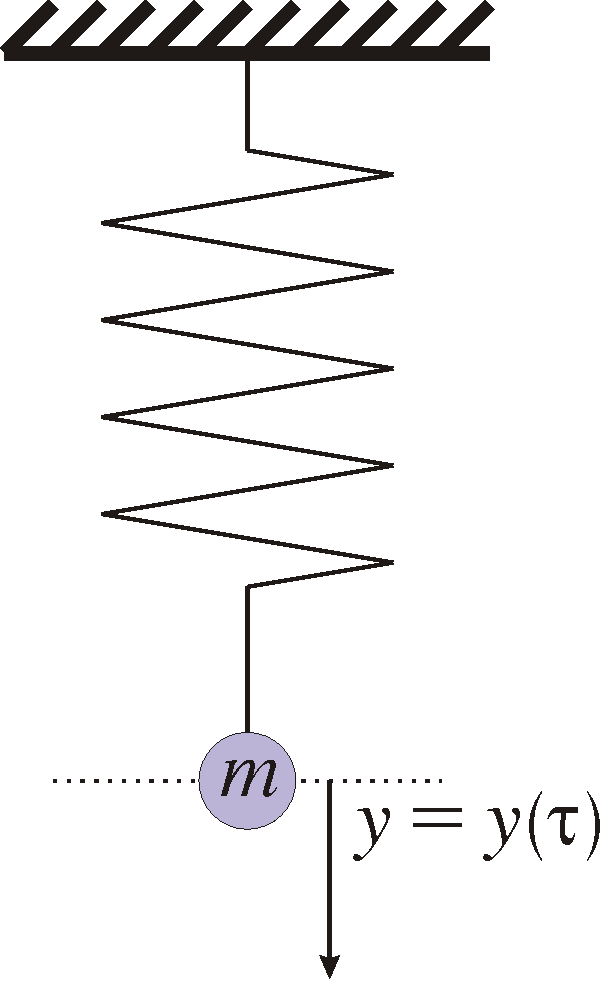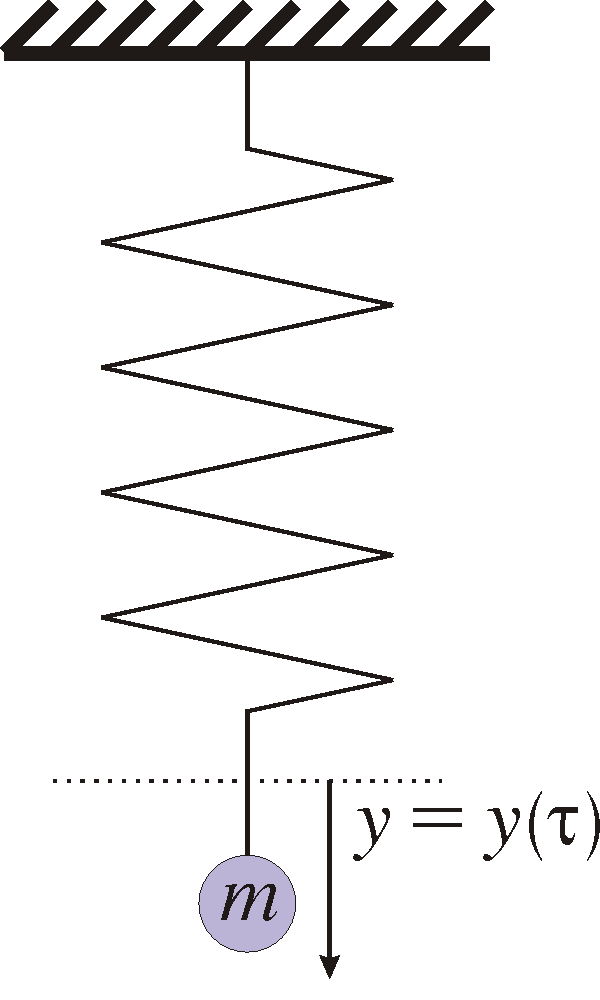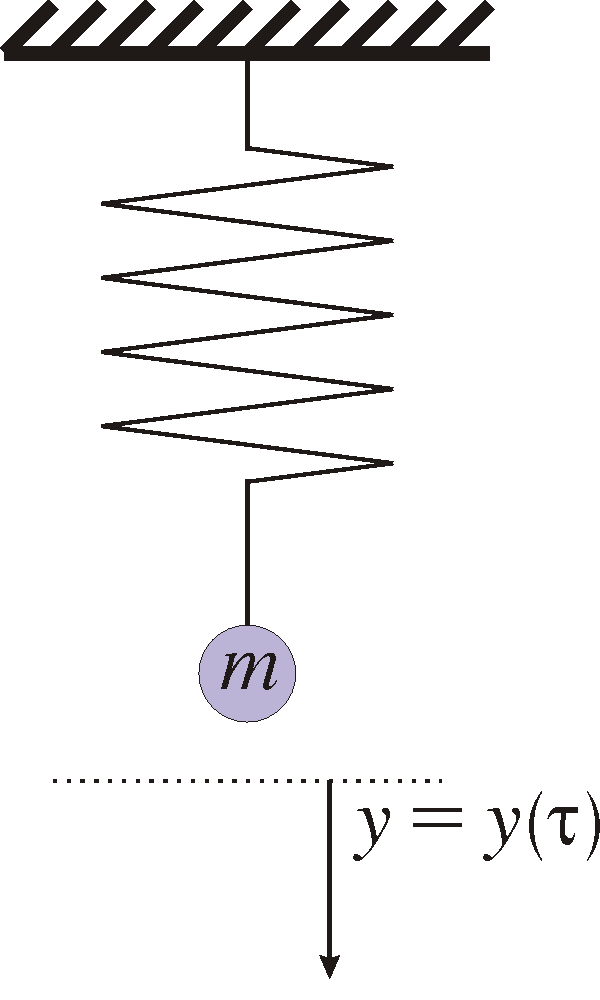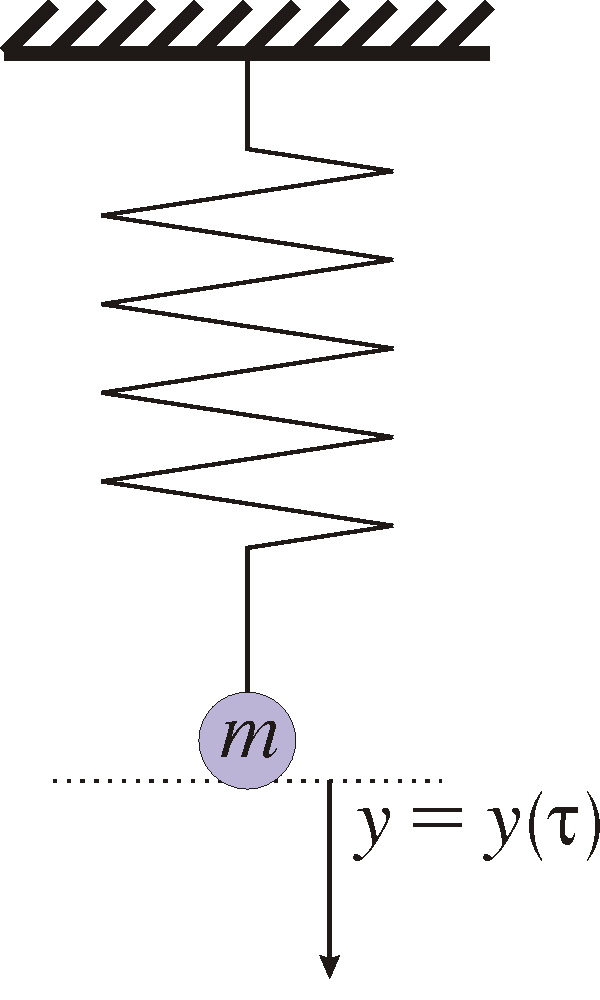
If y=y(t) denotes the distance from the equilibrium point, then the kinetic energy is
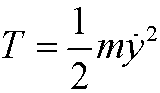
and the potential energy is
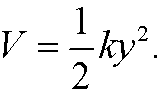
The Lagrangian is thus
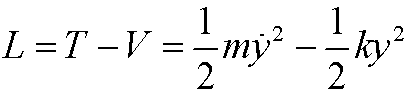
and the action integral
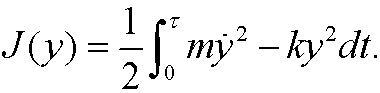
We have
when Lagrange’s equation
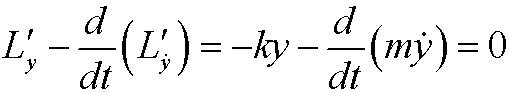
is fulfilled, that is, when
This is exactly Newton’s second law for the harmonic oscillator. Hamilton’s principle states that the motion will occur according to the above differential equation, with solution
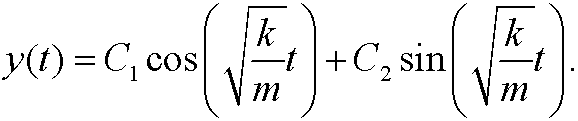
Finally we note that the Hamiltonian is
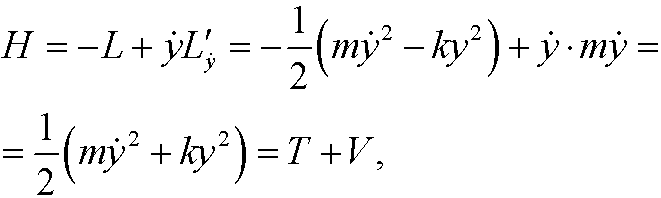
the sum of the potential and kinetic energies, that is, the total energy.
Example 2: (Simple pendulum.) Consider a mass m suspended in a pendulum of length l. We denote the angle from the vertical line with 
and the arc length from the equilibrium point with s.
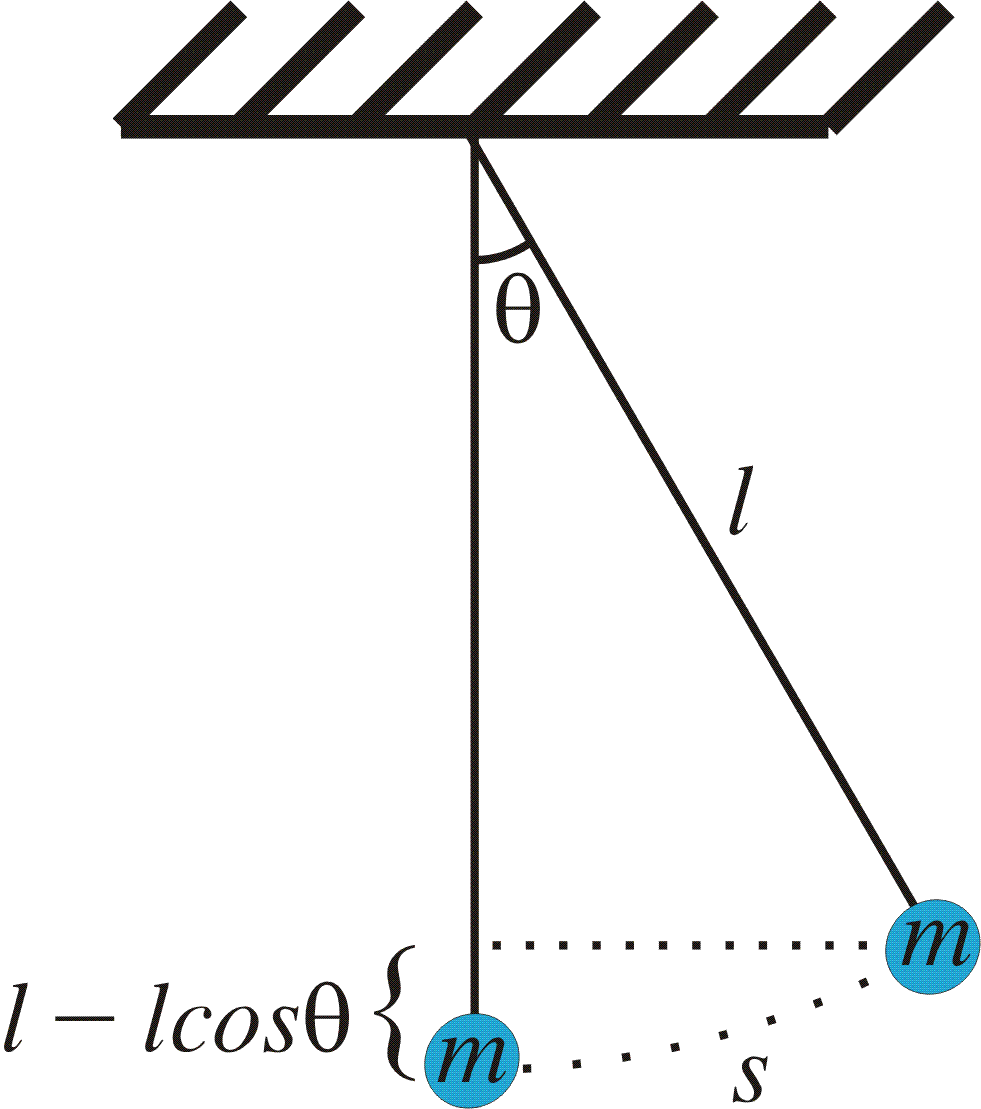
The arc length s is connected to the angle by
Then we have the kinetic energy
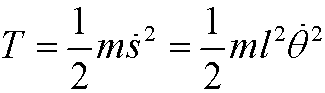
and the potential energy
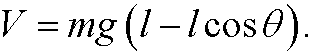
Hamilton’s principle states that the motion will be such that the action integral
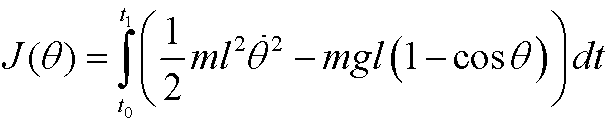
has a stationary value. Lagrange’s equation is in this case
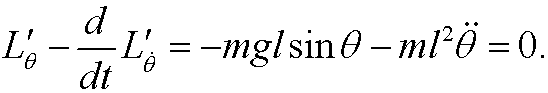
This implies that the equation of motion for the pendulum is
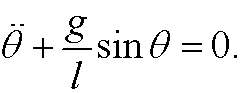
The Hamiltonian is in this case
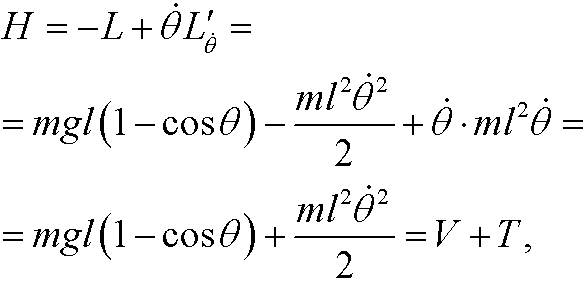
that is, the total energy of the system.
Example 3: (Motion in a central force field.)
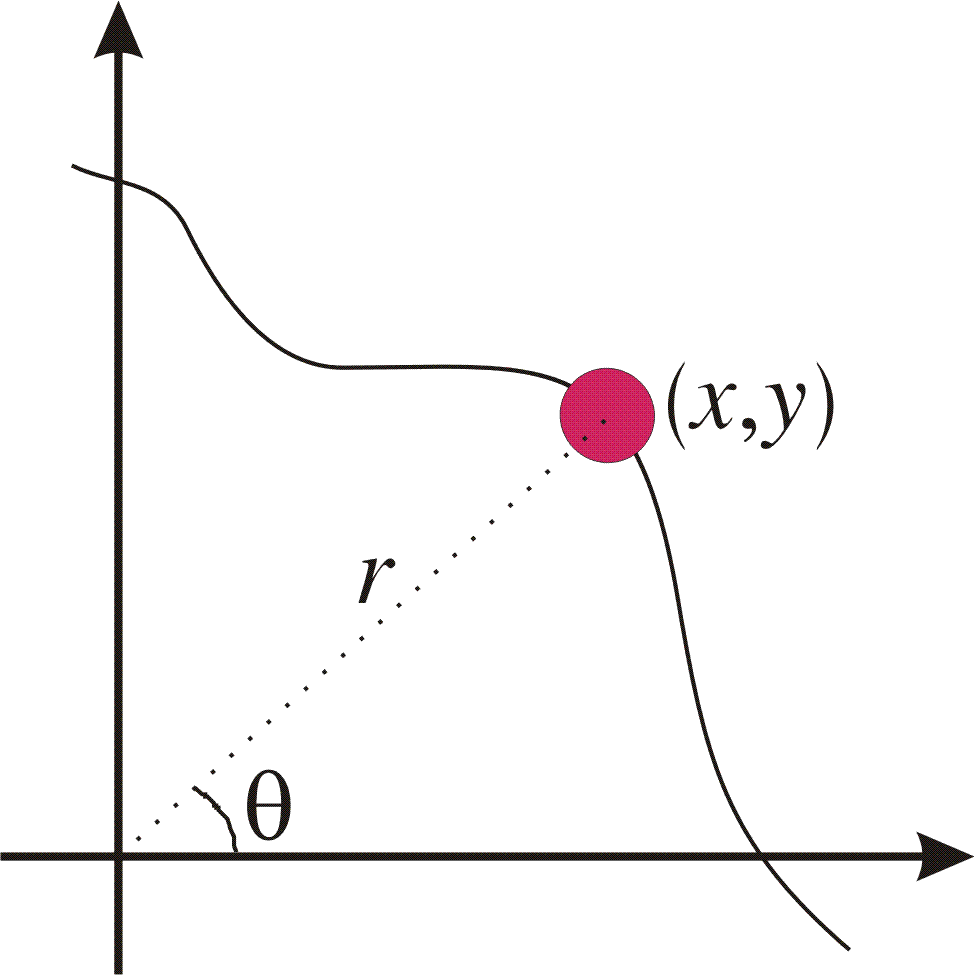
Let us examine the motion in the plane of a mass m that is affected by a tensile force towards that is reciprocal to the square of the distance to origo, that is
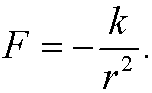
As generalized coordinates we choose the polar coordinates r=r(t) and 
. They are connected to the cartesian coordinates x and y by
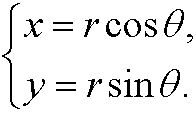
This means that the kinetic energy for the system is
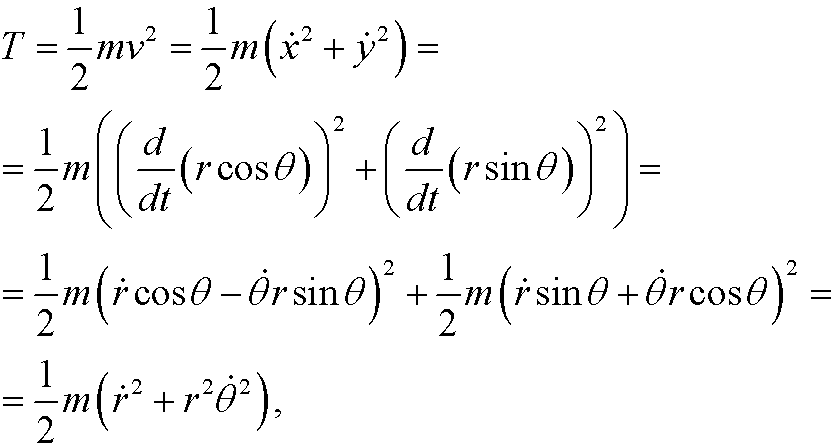
and the potential energy is (up to an additive constant)
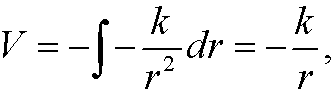
(since the force is the negative gradient of the potential energy.) The Lagrangian is thus
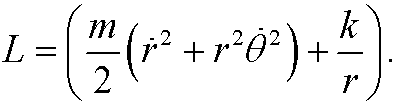
Hamilton’s principle now states that we should find
where
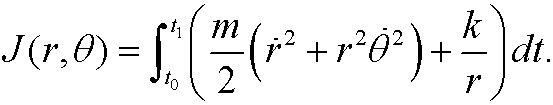
In this case, Lagrange’s equations become
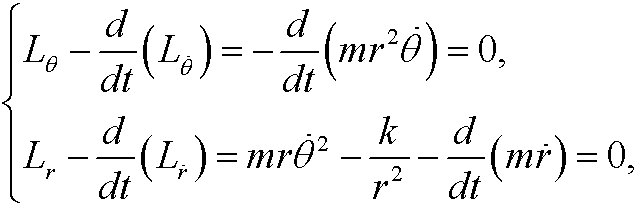
that is
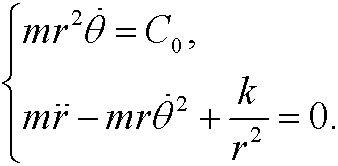
This coupled system can be solved exactly (leading to Kepler’s laws), but it is out of the scope of this course.