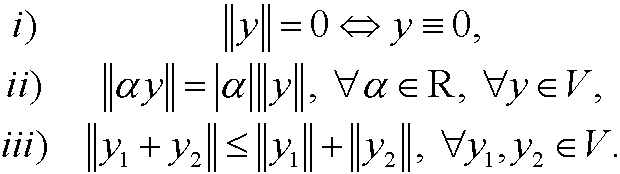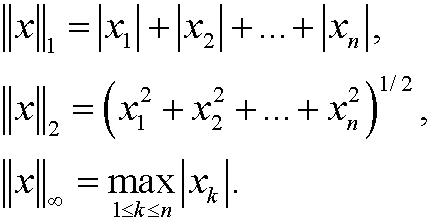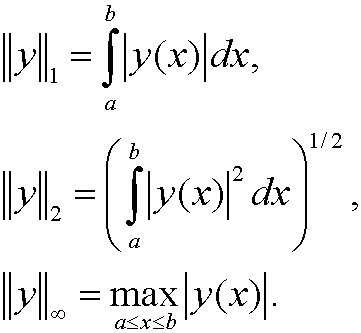A collection V of objects (functions, vectors,…) is called a real linear space if
a) there is an operation + on V such that if u and v belong to V then so does also u+v,
b) the operation + is commutative: u+v=v+u,
c) the operation + is associative: u+(v+w)=(u+v)+w,
d) there is a zero element 0 in V such that u+0=u for all u in V.
e) for every u in V there is an inverse denoted -u such that u+(-u)=0,
f) for all u in V and all a in R the scalar multiplication au is defined and belongs to V,
g) the scalar multiplication is associative and distributive:
h) 1u=u for all u in V.
Example 17: The set Rn.
The objects are the n-tipels x=(x1,x2,…,xn) where xk belong to R. The operation + is defined via
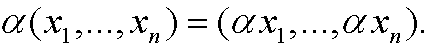
Example 18: The set C[a,b].
The objects are all continuous functions f on [a,b]. The operation + is defined via
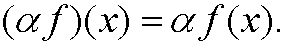
Example 19: The set Cn[a,b]. Analogously as example 18 above.
Example 20: The set V of all 2×2 matrices
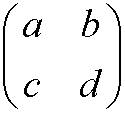
Proof: It is enough to find one counter example. Pick
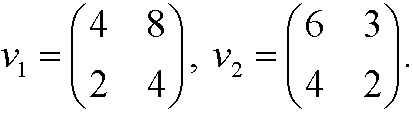
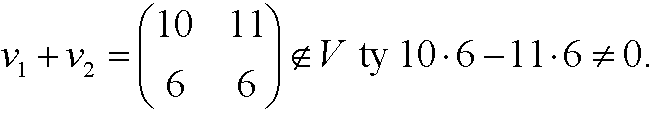
A normed linear space is a linear spaceV equipped with a norm. A norm is a mapping that to every element y in V maps a nonnegative number ||y||that fulfills the conditions