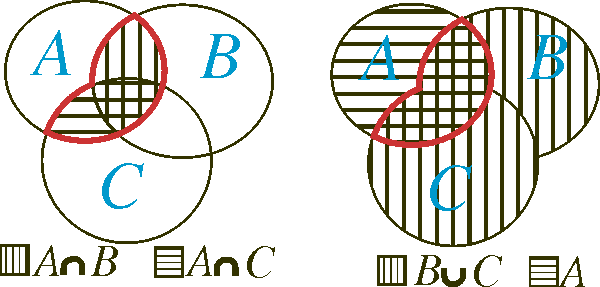A set is a collection of (arbitrary) objekt called elements. Assume that the elements in our set are the numbers 0, 2, 4, 6. We denote a set A by putting the elements inside the brackets
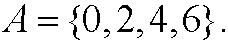
Element 2 belongs to the set A, but this is not true for 5 (for instance). We denote “belongs to” with  , that is
, that is
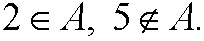
We do not make any difference in what order the elements appear, nor does it make any difference if one element is repeated. This means that also
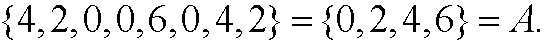
We can now define the cardinality |A| of the set as the number of uniqueelements in A. In the example above we have |A|=4. We can also defina a set by specifying its properties (read “the set of all k such that k=2n where n is an integer between 0 and 3”)
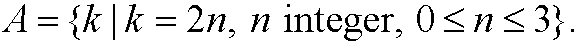
If we have defined a universe U (in this case that could be the set of all integers or the set of all reals), we can depict the set in a Venn-diagram
A subset B of a set A is a set that is attained by picking elements from the A. For example are all these sets
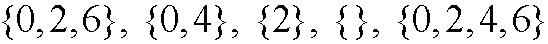
subsets of A above. We write
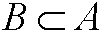
and depict it in a Venn-diagram as
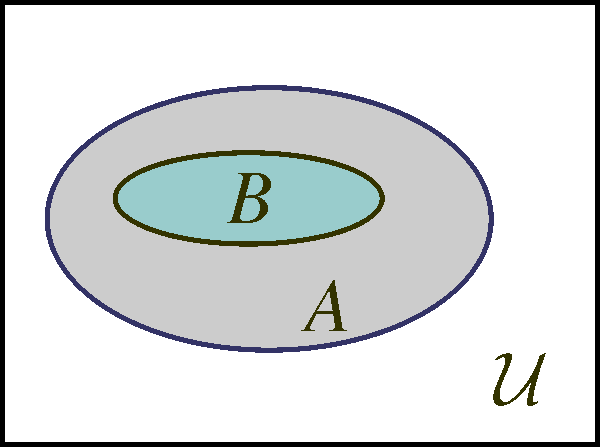
If two sets A and B have common elements, we say that they intersect. The set of the common elements is called the intersection and is written
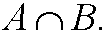
Two sets that do not intersect (have empty intersection) are called disjointsets. The set that is formed by taking all elements in both A and B is called the union and is written
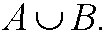
We define the set difference
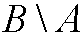
between B and A by taking all elements in B that are not in A. In such way we can construct the complement Ac to a set A (relative the universeU) as
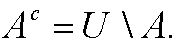
Example 1. Take the sets
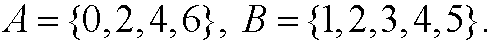
We can illustrate them as
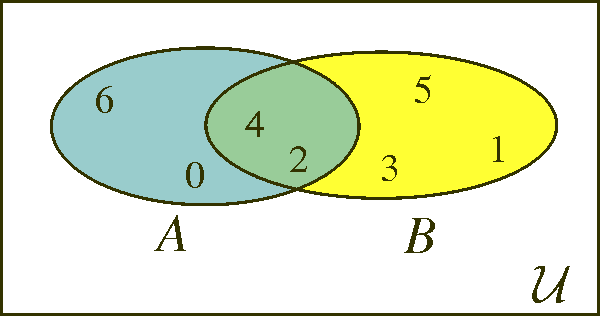
Then |A|=4, |B|=5, and
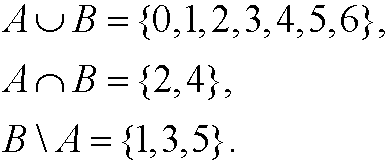
We illustrate this in the Venn-diagrams below
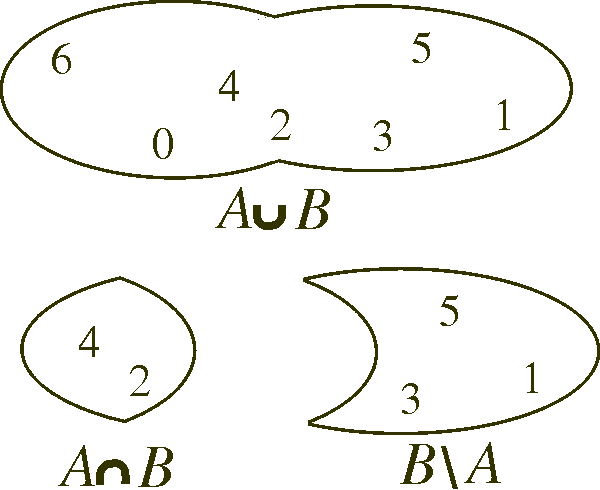
Moreover, if we let the universe U be the natural numbers (the set of all positive integers), we get the complement Bc as
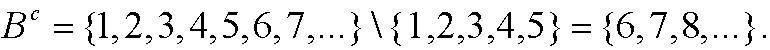
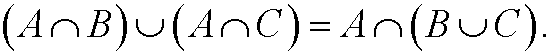
We can for instance use Venn-diagram to prove those, see the figure below.