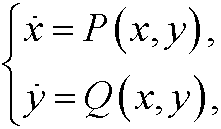7. Classification of critical points.

An equilibrium point to a system

 

i said to be isolated if there is a neighborhood to the critical point that does not any other critical points. There are four different types of isolated critical points that usually occur. They are center, node, saddle point and spiral.

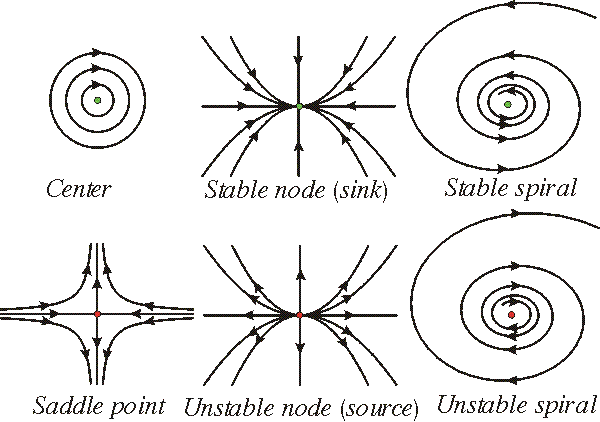
An equilibrium point can be stable, asymptotical stable or unstable. A point is stable if the orbit of the system is inside a bounded neighborhood to the point for all times t after some t₀. A point is aymptotical stable if it is stable and the orbit approaches the critical point as 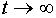 . If a critical point is not stable then it is unstable. In the figure above we see that a center is stable but not asymptotically stable, that a saddle point is unstable, that a node is either asymptotically stable (sink) or unstable (source) and that a spiral either is asymptotically stable or unstable.

 

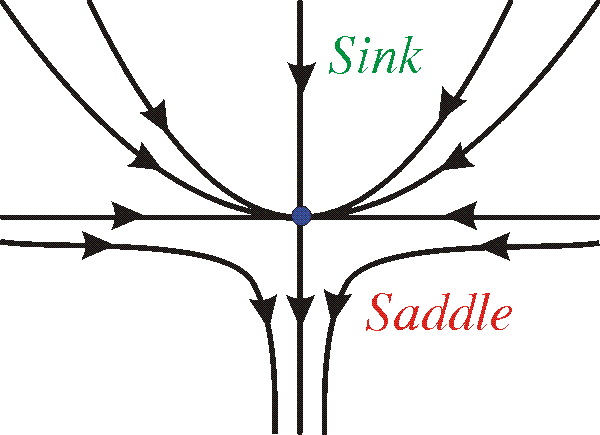
In certain nonlinear systems we might also have “mixtures” of the above types for higher order critical points. See the example above.