During some of the first years of the second world war, the mathematician G. I. Taylor (see also here) was given the task to compute how much energy will be released during an atomic bomb explosion. In such an explosion, a huge amount of energy is released in a very short time and in a region small enough to be considered a point. A powerful spherical chock wave spreads outward from the center. The pressure behind the wave is so immensely much higher than the surrounding pressure that it will not influence the chock wave particularly much. It is thus reasonable to assume that there can exist a physical relation
between the radius r of the chock wave, the time t after the explosion, the original density 
of the air and the released energy e. The Pi-theorem then guarantees that there is an equivalent physical law between the independent dimensionless quantities that can be formed from r, t, e and . We create the variable
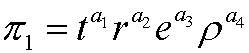
and search for the exponents a1, a2, a3 and a4 that will make the variable dimensionless. The original variables have the following dimensions:
| Symbol: | Quantity: | Dimension: |
| t | time | T |
| r | length | L |
| e | energy | ML2/T2 |
|
density | M/L3 |
where M is the dimension of mass. The dimension of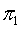 
is then
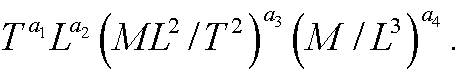
For to be dimensionless, we must have that
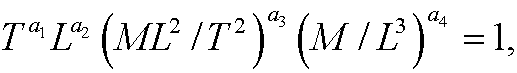
that is
For this to be possible, the exponents for T, L and M must all be 0. This can be written as the equation system
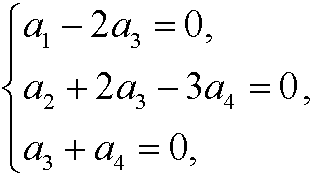
with the solution
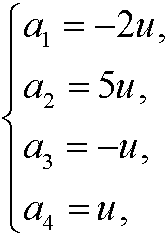
where u is an arbitrary real number. If we for instance let u=1 we get
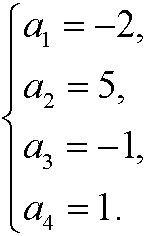
We then have the dimensionless variable
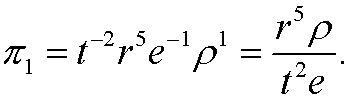
Since we only have one linearly independent solution we get one dimensionless variable and our physical law can be written
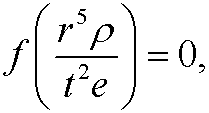
or
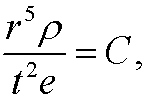
where C is a constant. If we solve for r, we get
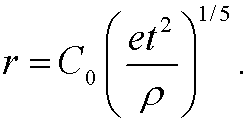
This dependence was later verified by a series of photographs (by J. E. Mack) taken in exact time steps after the first nuclear explosion in New Mexico 1945.
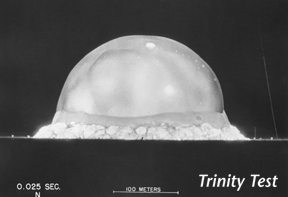
The released energy could finally be computed by curve fitting.