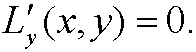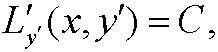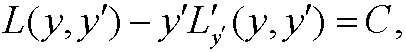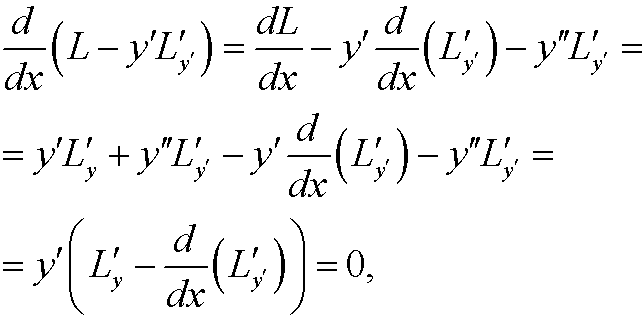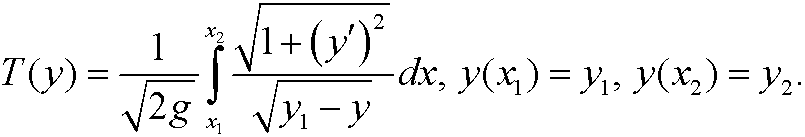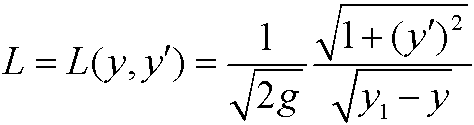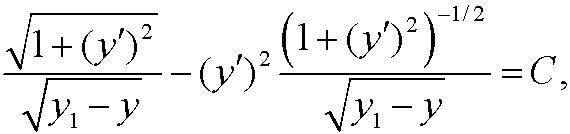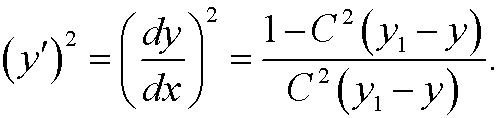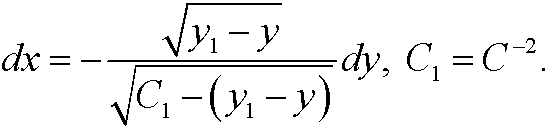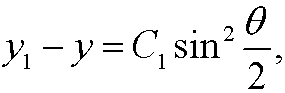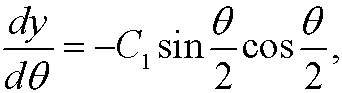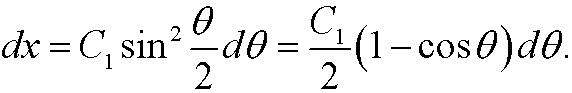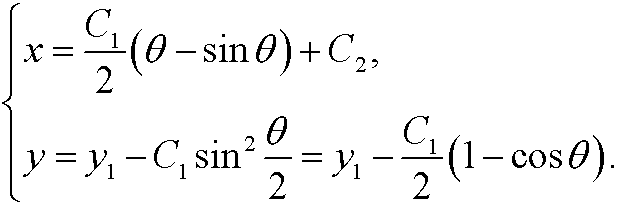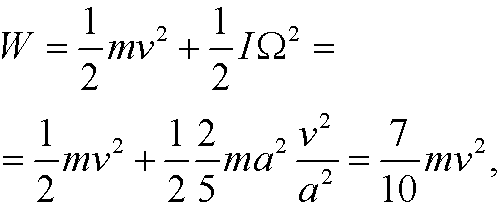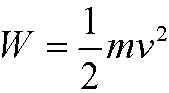7. Simplification of Euler´s equation.
Assume that the Lagrangian L=L(x,y,y‘) only depends on two of the three variables x, y andy‘. Then we can simplify Euler’s equation somewhat. We have the following three special cases:
Case 1: L=L(x,y). Then Euler’s equation is
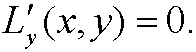Case 2: L=L(x,y‘). Then Euler’s equation is
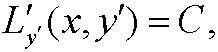where C is an arbitrary constant.
Case 3: L=L(y,y‘). Then Euler’s equation
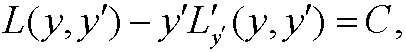where C is and arbitrary constant.
Remark: The relation in case 3 above is called Beltrami’s identity.
Proof (Case 3):
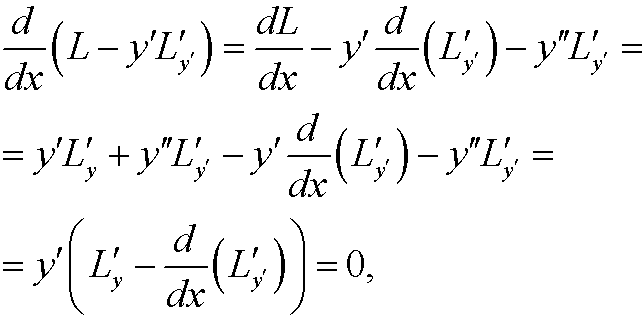where equality in the last step follows from Euler’s equation.
Example 12 (Compare example 5): Find the extremal to the functional
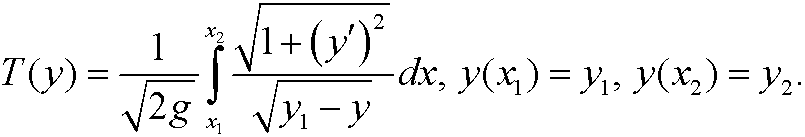Solution: Here
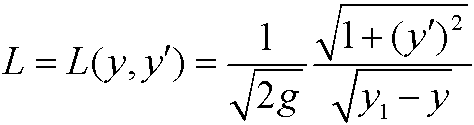and we can thus simplify the problem by using Beltrami’s identity above. We get
which can be simplified to
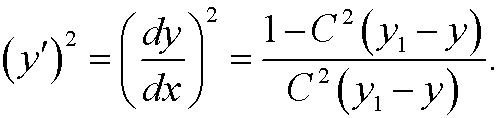This implies that
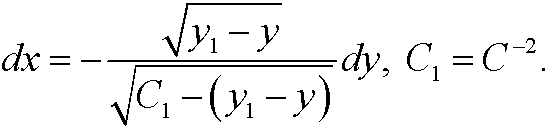We choose minu sign above since dy/dx<0 (see the figure). Now make the change of variables
<>
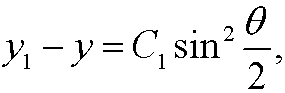
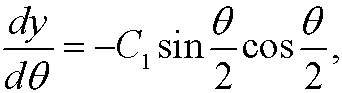
with which the equation becomes
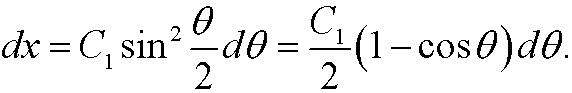Integration thus yields
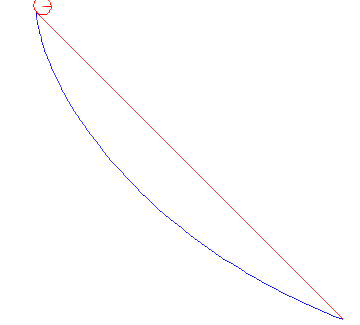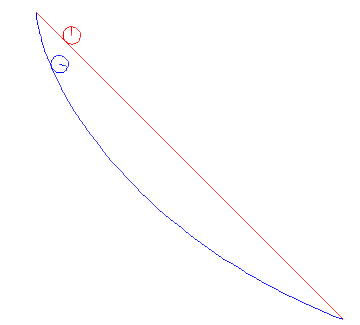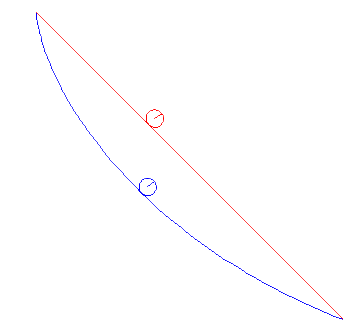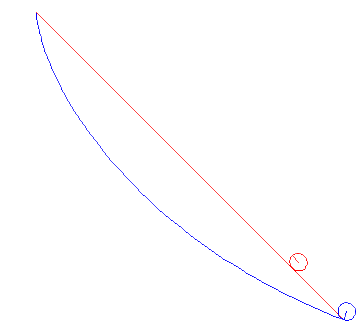
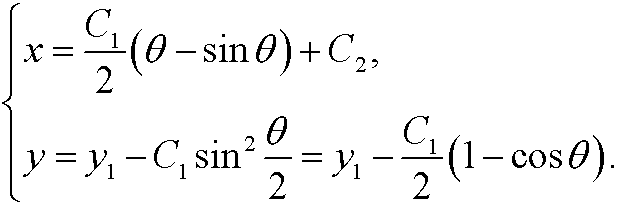Th constants C1 and C2 are chosen such that the boundary conditions are fulfilled. This is the parameter form of a cycloid, the curve that describes how a point of the circumference of a wheel as the wheel rolls along a straight line. See the figure below:
In the animations below, we cinsider a ball of radius a rolling between two points under gravity. We compare the cases when it is rolling the shortest way and when it is rolling along the cycloid that passes through both points. It is obvious that the cycloid gives shorter time of descent than the straight line, but there are also differences depending on the average slope between the start and end points.
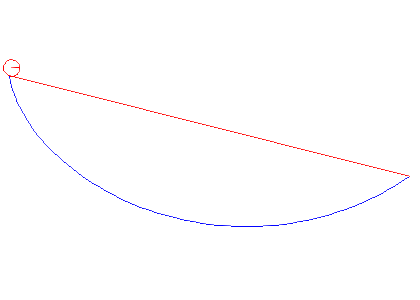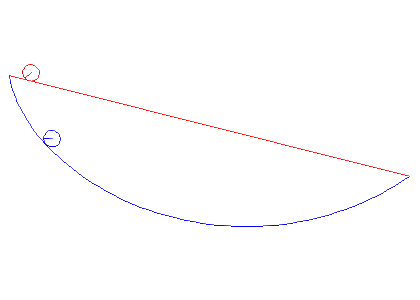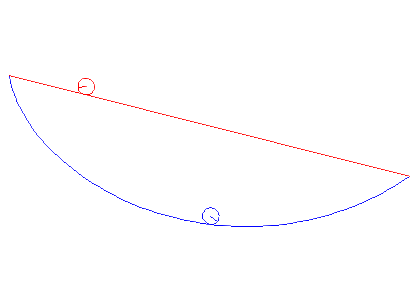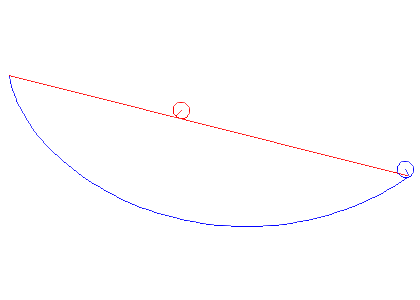Note that problem we solved above actually deals with a particle gliding along a curve, but the correction we have to do for a rolling ball is that the kinetic energy W instead is given by
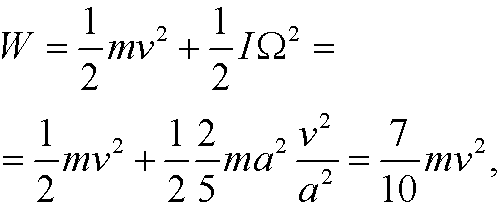where I is the moment of inertia of the ball and 
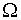its angular velocity. If we use this expression instead of
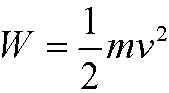in example 5 we easily realize that it leads to the same differential equation and thus the same solution.
Remark: The cycloid also has the interesting property that it is tautochrone. That means that a particle placed anywhere on the cycloid will glide along the curve under gravity to the lowest point in the same amount of time, regardless of where it started. This property is illustrated in the figure below:
