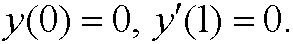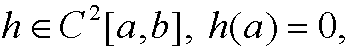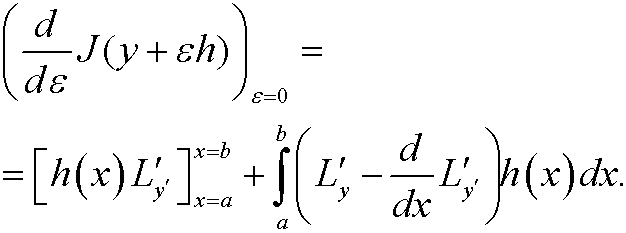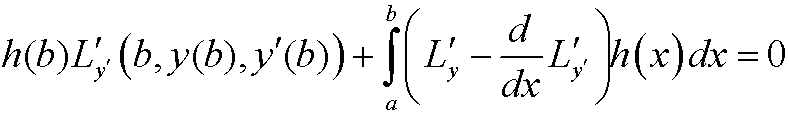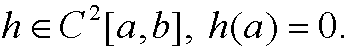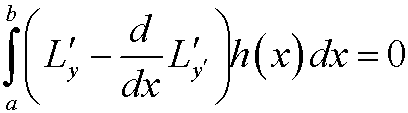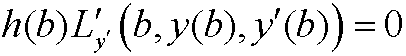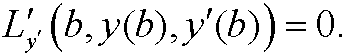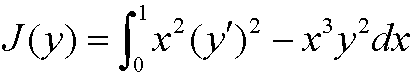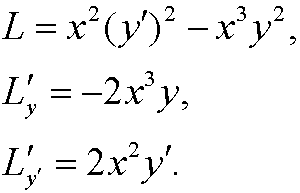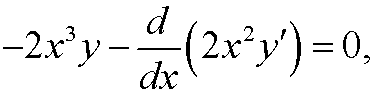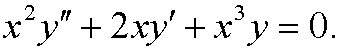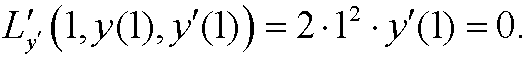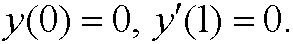9. Natural boundary conditions.
Assume that we instead had the boundary conditions y(a)=y0, y(b)undetermined, in theorem 1. Such a problem is called a free-boundary value problem. Now choose the function h such that
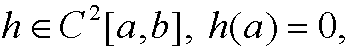without posing any condition on h in the point x=b. By imitating the proof of the original theorem we see that
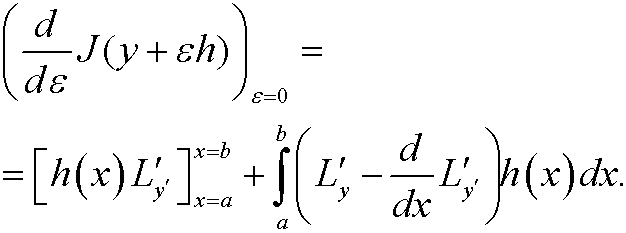Since h(a)=0 a necessery condition for y to be extremal is
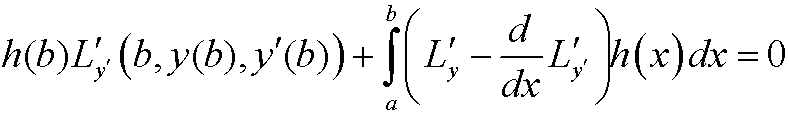for every
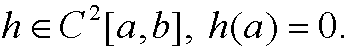Since this condition holds for all h above, it in particular holds for those hthat fulfills h(b)=0. This implies that
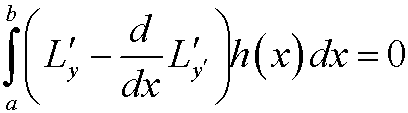and by the lemma in the previous part, we realize that y must fulfill the Euler equation
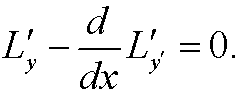
If we again let h(b) be arbitrary and return to the necessary condition above we see that when we insert the Euler equation that we must have
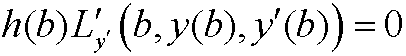(for all choices of h(b) ). Since this is independent of h(b) we must have
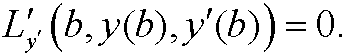This is the natural boundary condition.
Example 13: Find the differential equation and the boundary conditions for the extremal to the functional
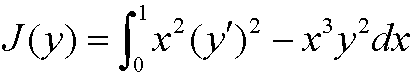when y(0)=0, y(1) undetermined.
<>
Solution:
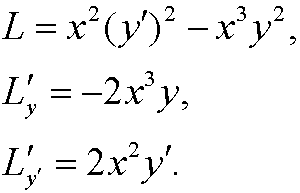The Euler equation is then
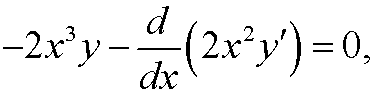that is,
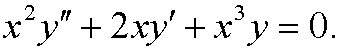The natural boundary condition in x=1 is
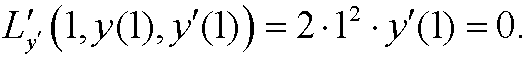This means that the boundary conditions are
