Problem: Minimize the functional
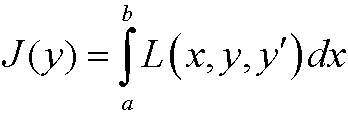
under the constraint
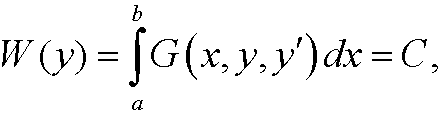
where
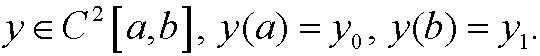
Method: In principle we follow the procedure from part 8 in the chapter about calculus of variations. We look for a local minimum y(x) in a family of admissible functions. However, we cannot use a one-parameter family 
like in chapter 3, since a change of the parameter in general would have implied that the value of the constraint W(y) would have changed. We instead introduce a two-parameter family
where
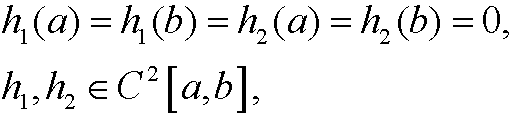
and 
are real parameters from an interval containing origo. We swap yfor z in the functionals and construct
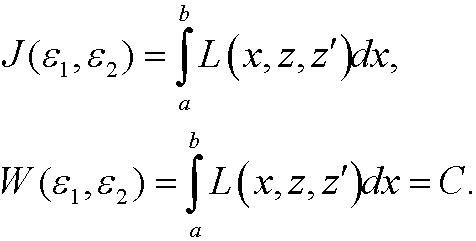
Obviously, these parameters are not independent, since W(y) must be a constant C we have the relation
between them. Since y(x) is an extremal, we must have an extreme value on J when 
. This is simply an extreme value problem with constraints, of the same type as we investigated in the previous part. We thus construct the function
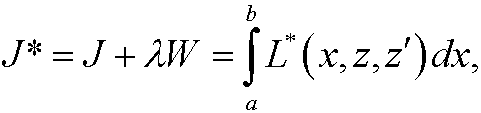
where
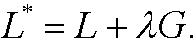
According to the theorem in the previous part we then have the condition
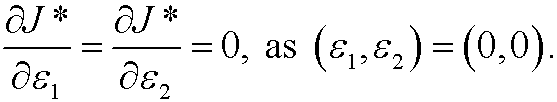
These derivatives are equal to (by the chain rule)
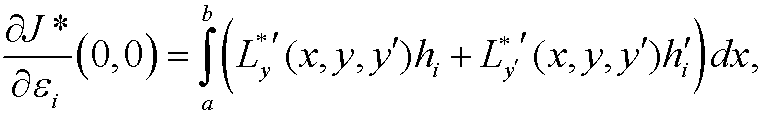
for i=1,2. We integrate by parts and use the boundary conditions on h1 and h2 and get
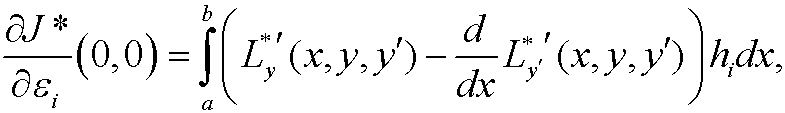
for i=1,2. With the lemma from part 8 in chapter 3 and the fact that h1 and h2 were arbitrary functions we get that
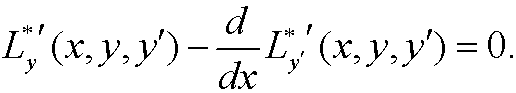
A necessary condition for minimum (extremum) is thus that L* fulfills Euler-Lagrange’s equation
Remark 1: The problem and its method of solution can be generilzed to higher dimensions and more constraints in a straightforward way.
Remark 2: The solution we get from Euler-Lagrange’s equation above often depend on two unknown constants and the multiplier 
. These can be determined by help of the boundary conditions and the constraint.