Example 7: Determine the shortest curve y=y(x), y(0)=a, y(1)=b, that spans the area A together with the coordinate axes and the line x=1.
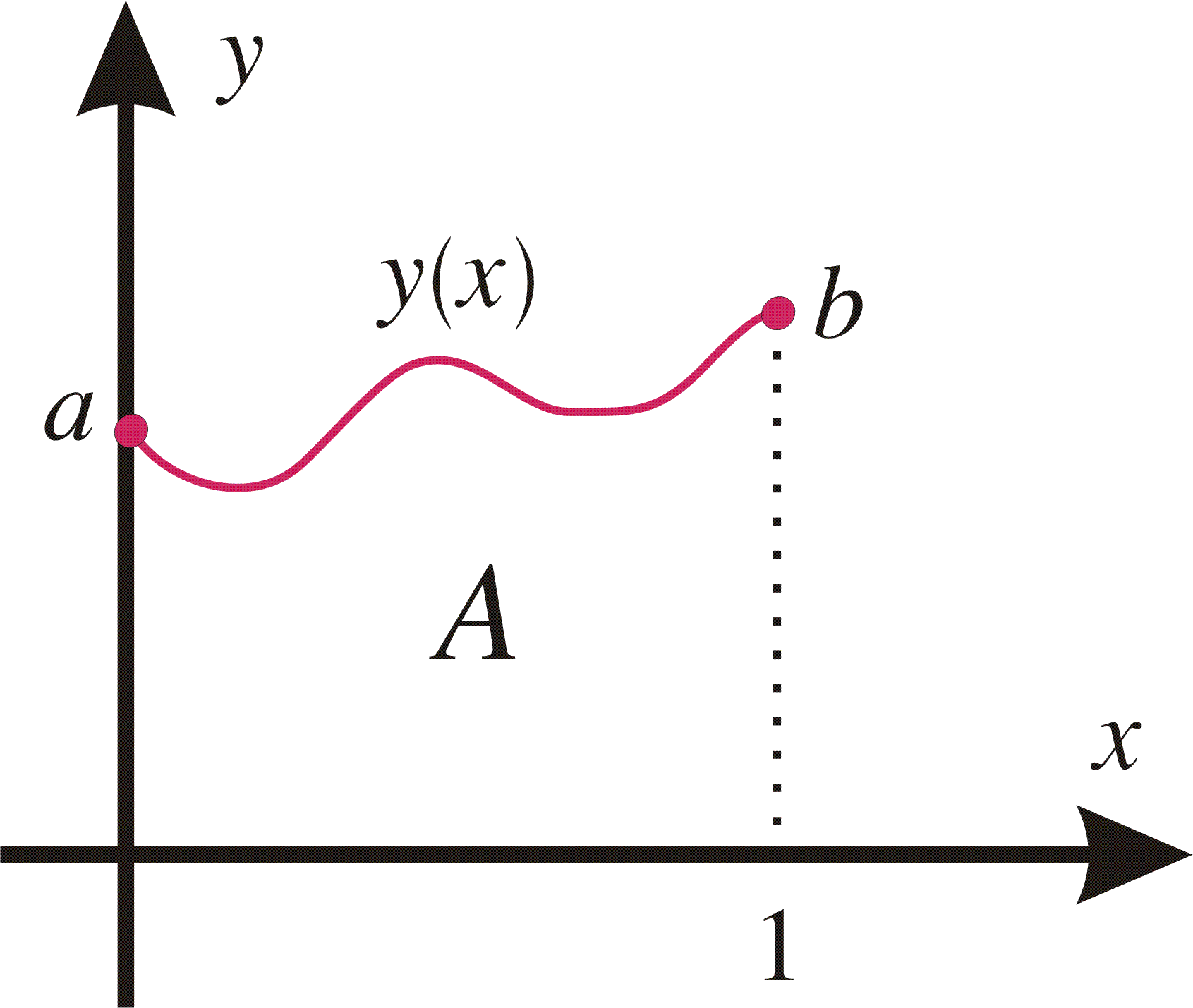
Solution: The problem thus means that we should minimize the functional
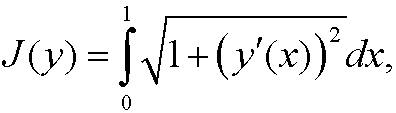
under the constraint
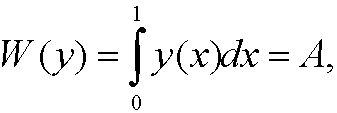
where
By using the method from the previous part we must construct the functional
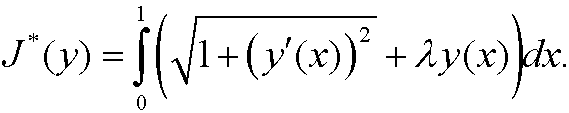
A necessary condition for minimum is that
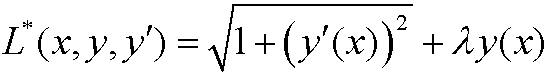
fulfills Euler’s equation
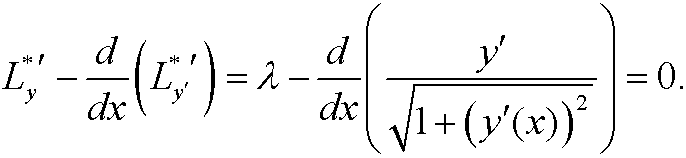
Integration now gives
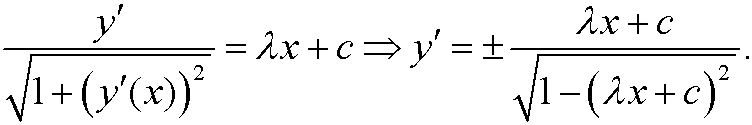
If we integrate again we see that
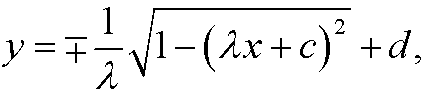
that is
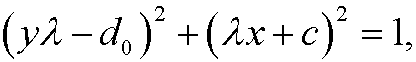
which is a circle. The unknown constants 
, d0 and c are deterermined from the three conditions
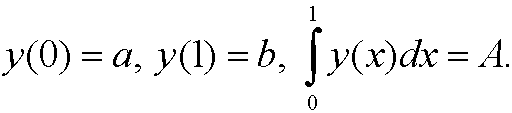
Example 8: (Chain line). A rope of length l and constant mass 
per unit length hangs between two fixed points (a,y1) and (b,y2) in the plane. What shape y(x) will the rope attain?
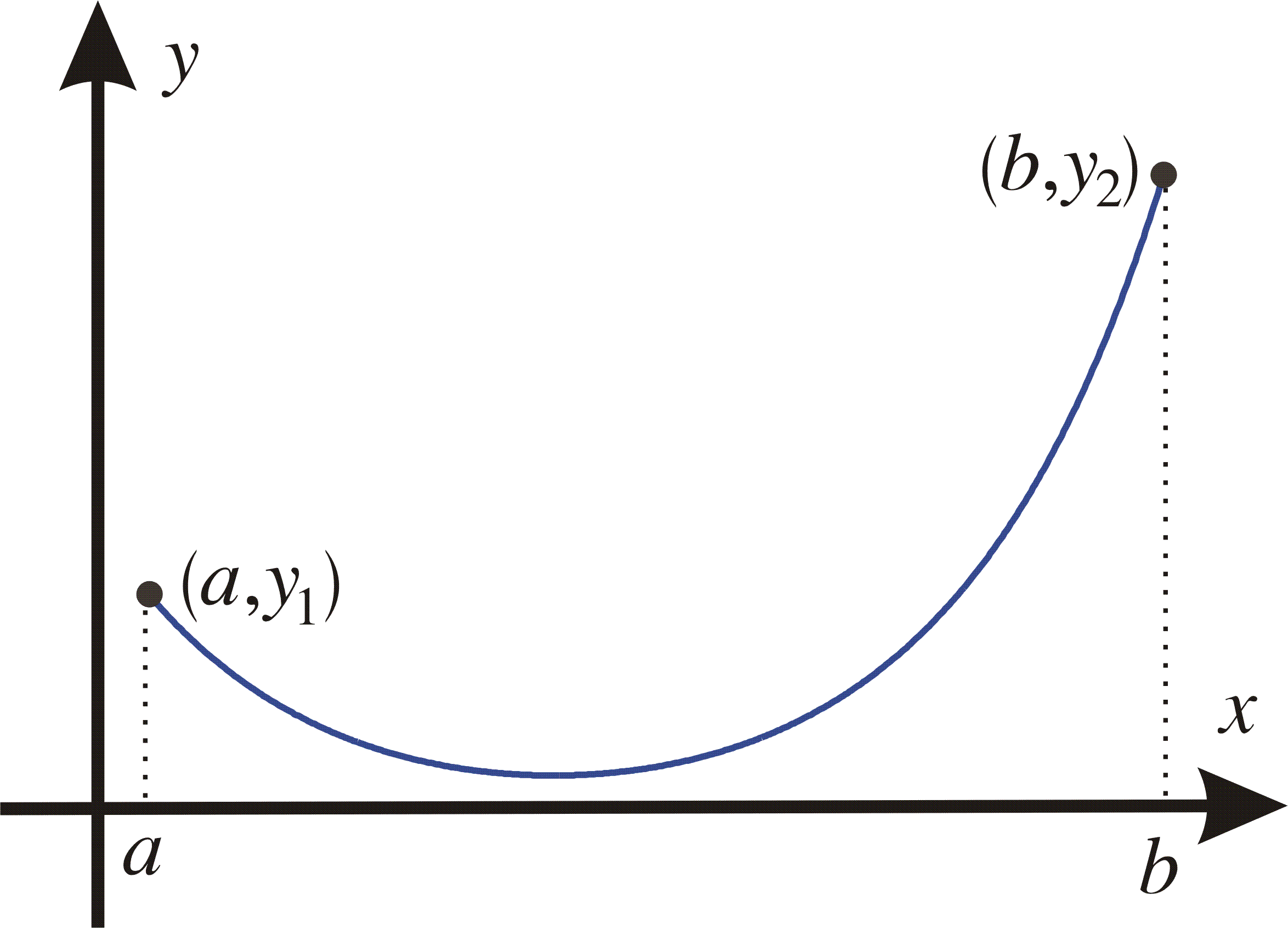
Solution: A small element ds in the point (x,y) has the mass
and the potential energy
with respect to y=0. The total potential energy is thus
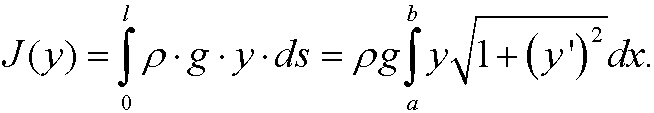
The rope assumes a shape such that the potential energy is minimized. This means that we should minimize J(y) under the constraint of constant length
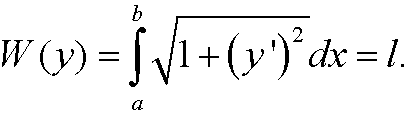
We thus construct
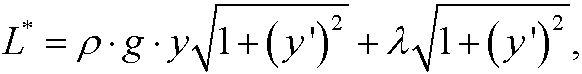
and put it into the Euler equation. However, in this case L* does not explicitly depend on x and we can thus use Beltrami’s identity
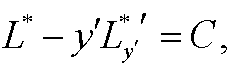
that is
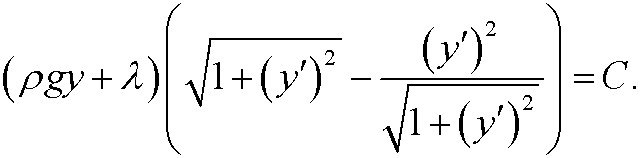
If we solve for y’ we get
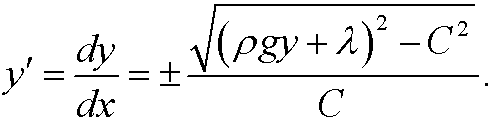
This is a separable differential equation. Hence integration gives
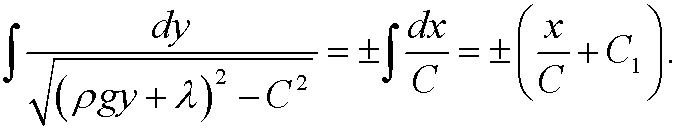
We now make the change of variables
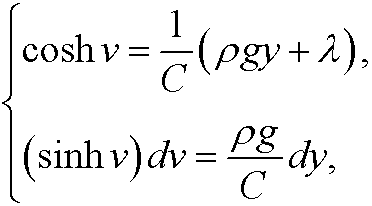
and then the left hand side integral transforms to
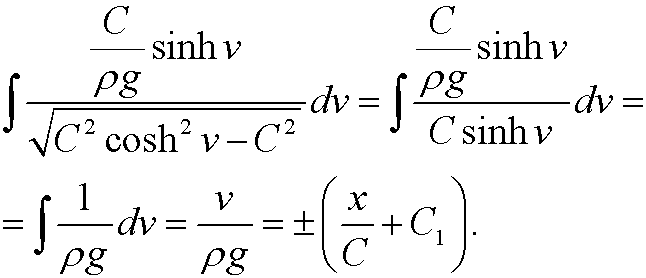
We multiply with 
and then take cosh(.) on both sides of the equality sign and use that it is an even function. We get
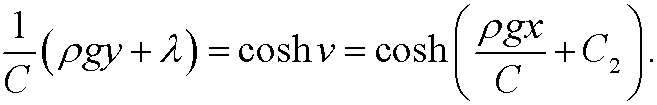
If we finally solve for y we get
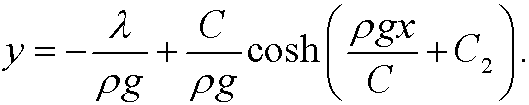
This means that the shape of a hanging rop is a catenary (or chain line). The constants C, C2 and are determined by the boundary conditions and the curve length.
Example 9: Find the extremals to the triple integral
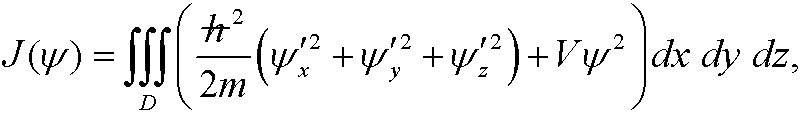
under the constraint
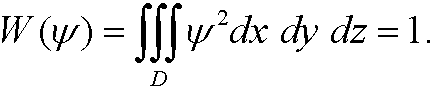
We thus construct
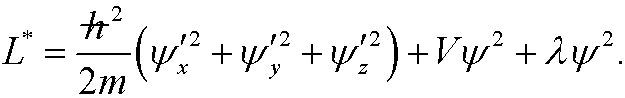
The Euler equation in this case becomes
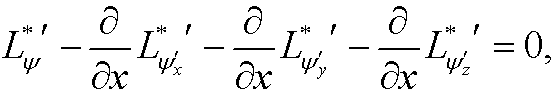
that is
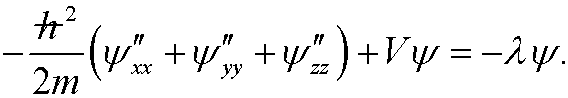
This is the famous Schrödinger equation in quantum mechanics for a particle of mass m under the influence of a potential V. In this case D is R3and the constraints is the normalized probability condition for the wave function 
, whose square is a probablility density (a measure of where a particle most likely will be). In general we can only find solutions for particular discrete values of the multiplier , identified as the possible energy levels that the particla may have.