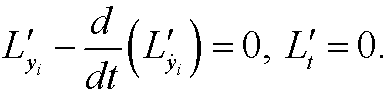According to Lagrange’s equations we have that
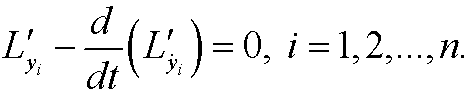
Now suppose that L is independent of t, that is, Lt=0. Then we can use a variant of Beltrami’s identitet (see below for derivation) and rewrite the equations as
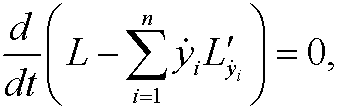
which by integration becomes
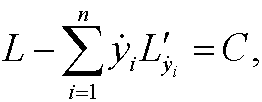
where C is a constant. This is called a conservation law and the quantity
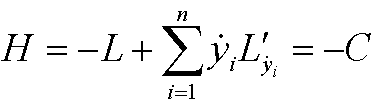
is called the Hamiltonian of the system. It normally represents the total energy of the system. The analysis above thus means that if L is time independent then the totla energy of the system is preserved.
Derivation:
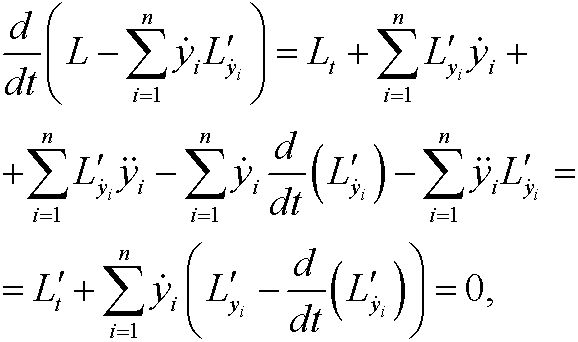
since