Consider the action integral
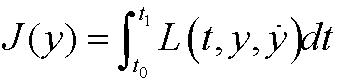
and the corresponding Lagrange equation

We define a new variable p, called the canonical momentum, by
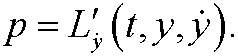
If
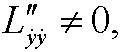
we might according to the implicit function theorem solve for ![]() as
as
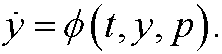
In particular we may write the Hamiltonian as
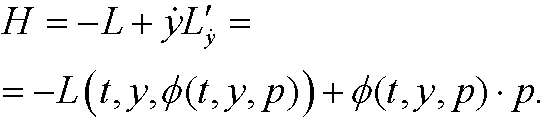
Example 4: Consider a particle of mass m and potential energy V(y), moving in one dimension. Then
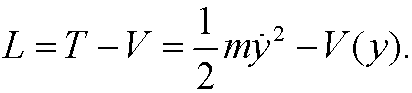
This implies that
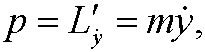
the regular momentum. If we solve for ![]() we get
we get
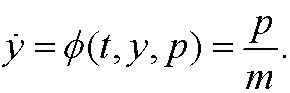
The Hamiltonian thus becomes
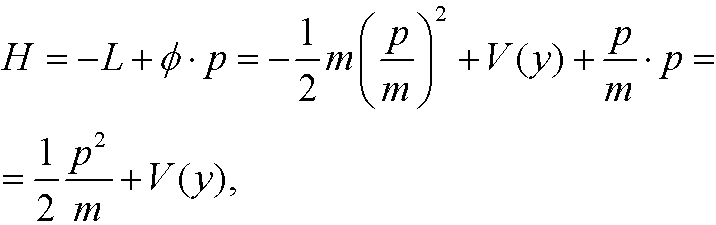
the total energi expressed in the position y and the momentum p.
We also note that
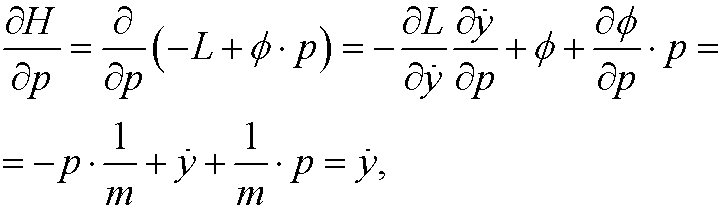
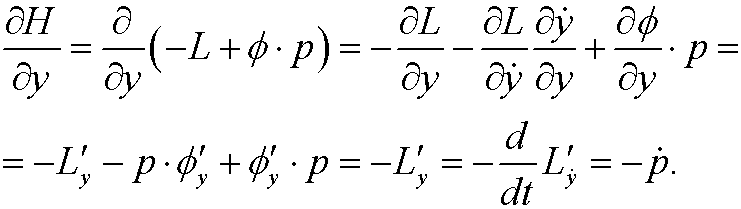
Lagrange’s equations can thus be written as a system of equations in the variables y and p,
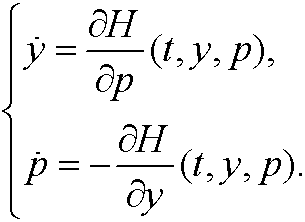
Definition: The equations above are called Hamilton’s equations.
Example 5: Consider the harmonic oscillator in Example 1. Then
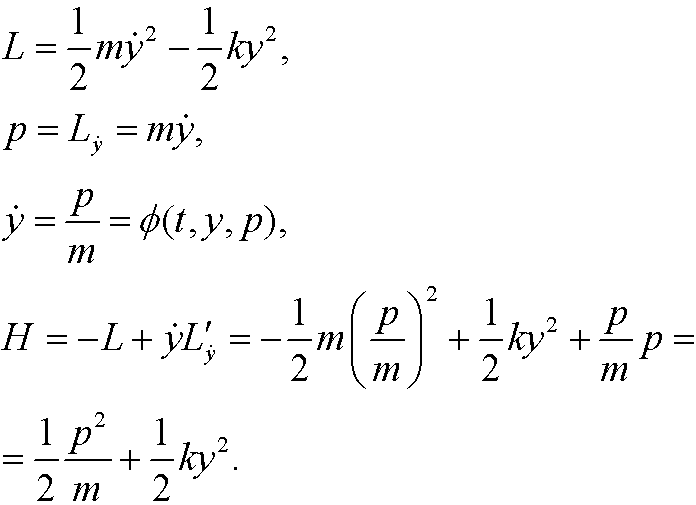
Hamilton’s equations are in this case
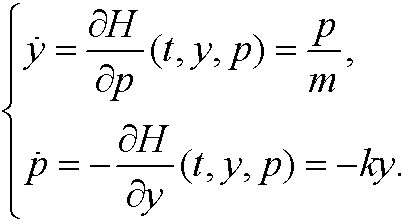
We solve these equations in the yp-plane (the so called phase plane). Division yields
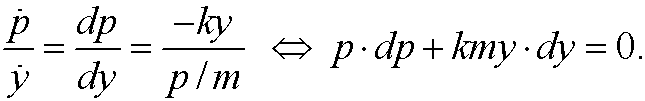
This is a separable equation. Integration gives
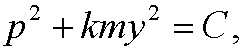
where C is a constant. Geometrically this is a family of ellipses in the phase plane.
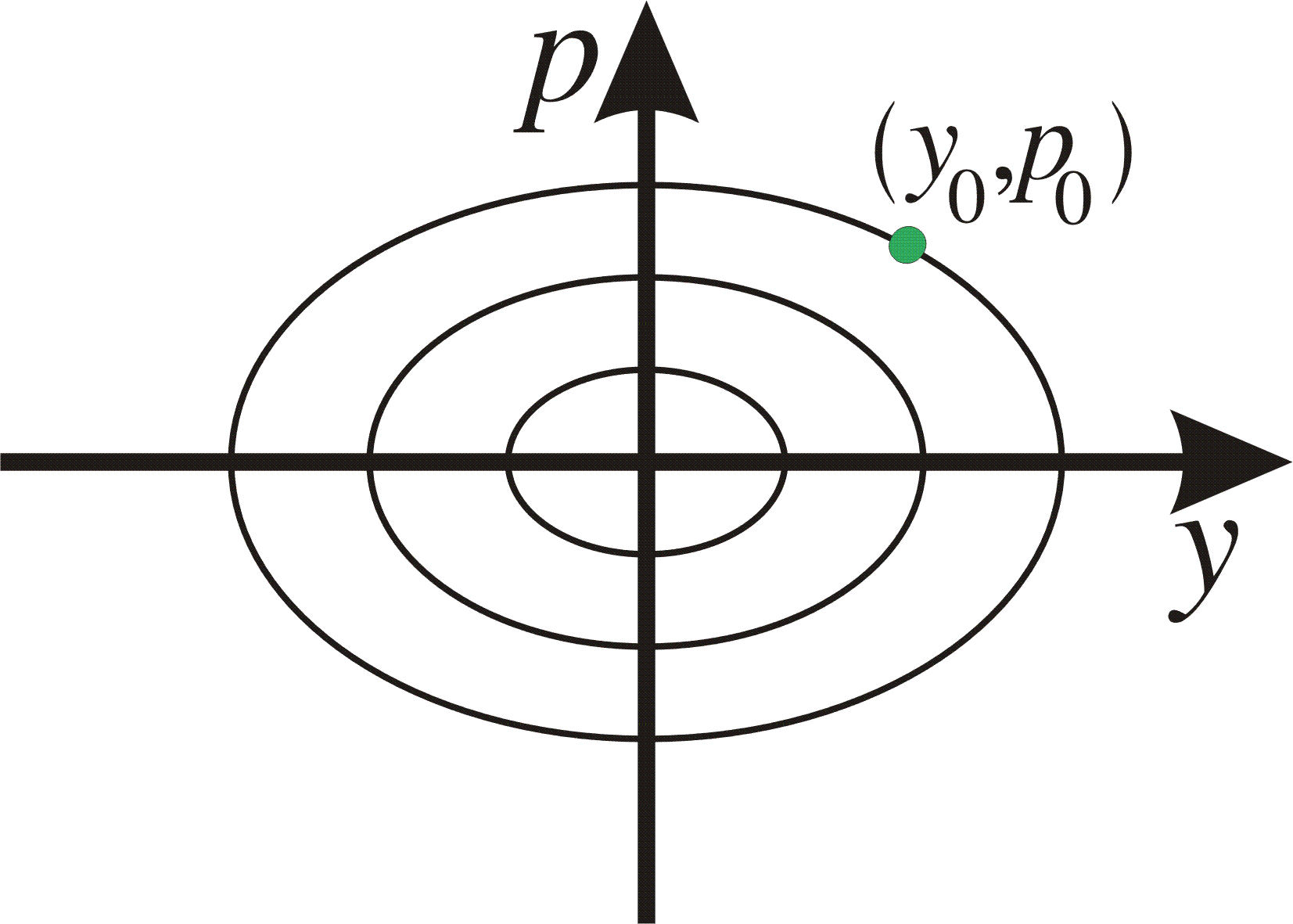
This are the curves the system develops along in the phase space.
Remark: Euler-Lagrange’s equation for the harmonic oscillator is
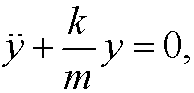
with solutions
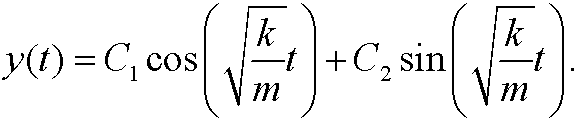
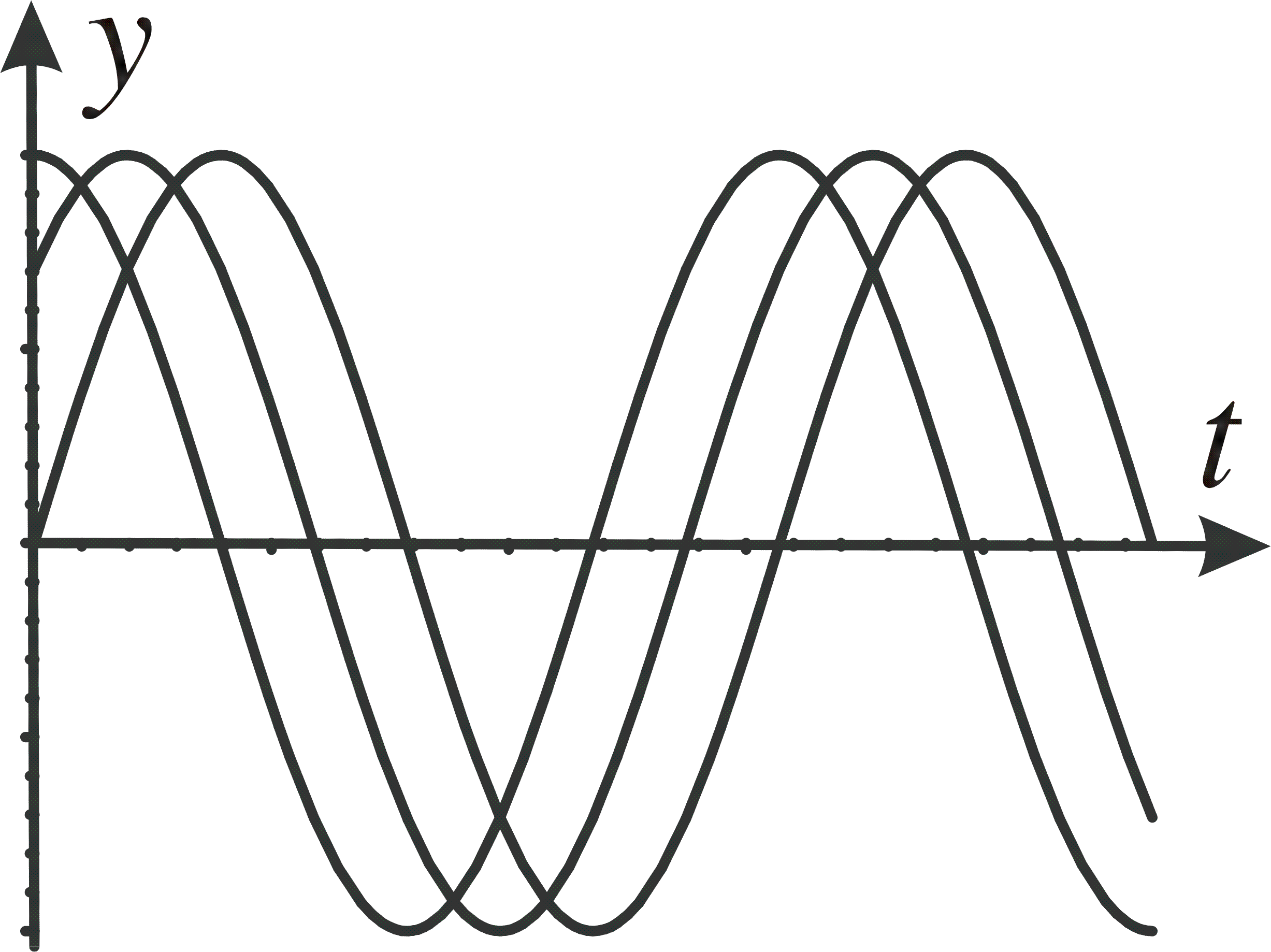
These solutions can also be represented in the yt-plane, shown below.