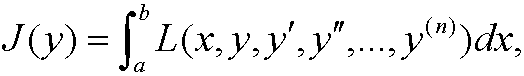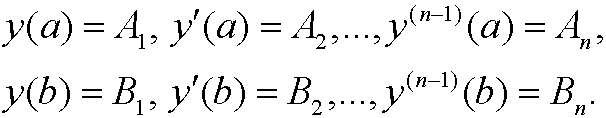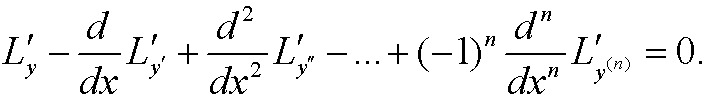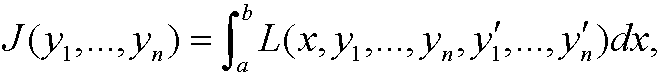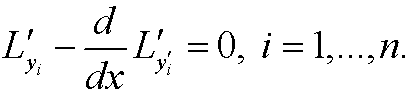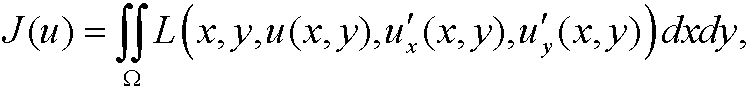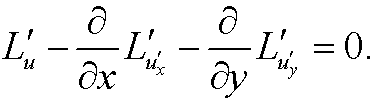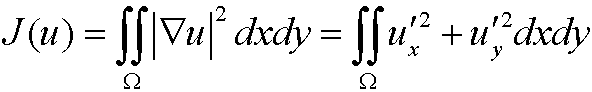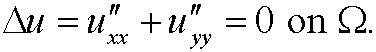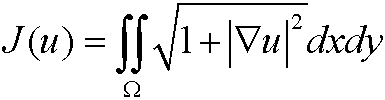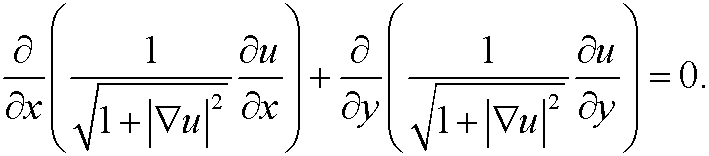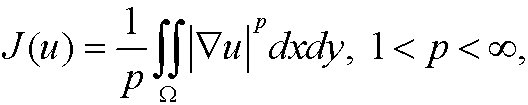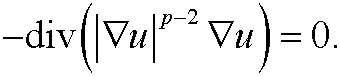10. The Euler equation for some more general cases.
1. Higher derivatives: Assume that we have a functional of the type
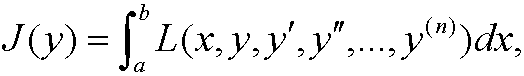where y is a function in C2n[a,b] that fulfills the boundary conditions
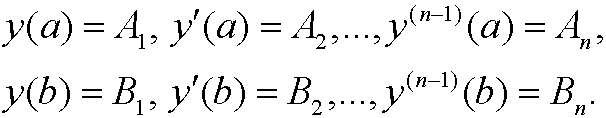The Euler equationen is then
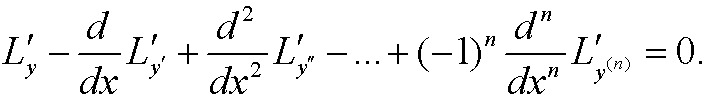2. Several functions: Assume that we have a functional of the type
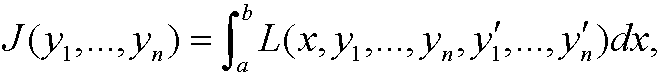where yi, i=1,…,n are functions in C2[a,b] that fulfill the boundary conditions
<>
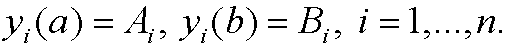
The Euler equation is then
<>
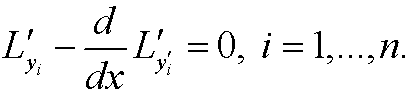
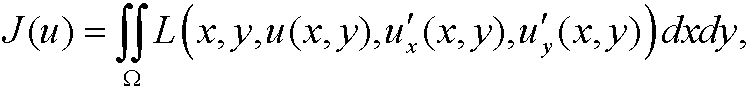where u is a function in C2(
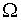) that fulfills the boundary condition
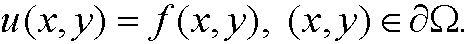The Euler equation is then
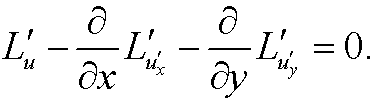Example 14: (Compare example 9.) The Euler equationen to
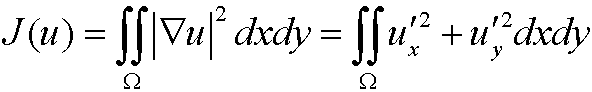is Laplace’ equation
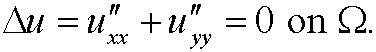Example 15: (Compare example 8.) The Euler equation to
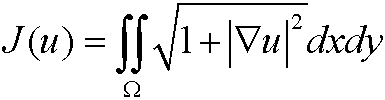is the nonlinear differential equation
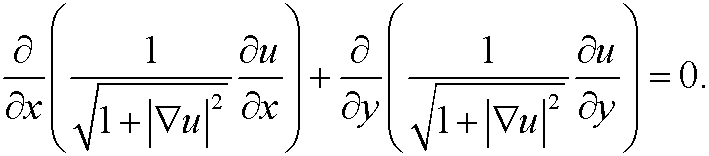Example 16: The Euler equation to the functional
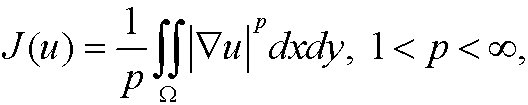is p-Laplace equation
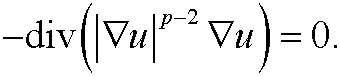This equation is also called the p-harmonic equation and is sometimes used to model non-Newtonian flows.
