Hamilton’s principle states that the development in time for a mechanical system is such that the integral of the difference between the kinetic and the potential energy is stationary. More specific we haver:
Hamilton’s principle: The motion of a mechanical system from time t0 to t1 is such that the functional
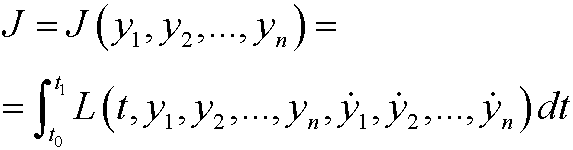
is stationary for the functions y1(t), y2(t),…,yn(t), describing the development in time for the system.
Here
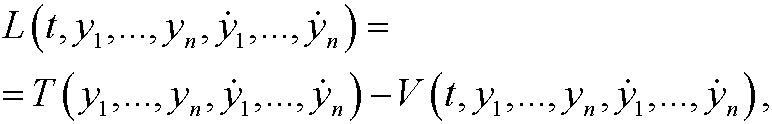
that is, the difference between the kinetic energy T and the potential energy V.
Remark 1: Hamilton’s principle is often mathematically expressed as
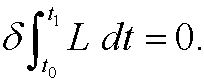
The quantity
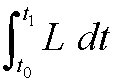
is called the action integral.
Remark 2: Hamilton’s principle mean that among all curves between the end points, the motion will occur along the curve that gives an extreme value (actually stationary value) to the action integral.
Remark 3: By using calculus of variations (see chapter 3) we see that yi(t)must fulfill the Euler equations
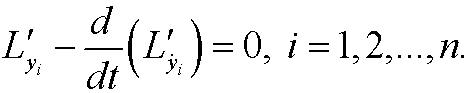
In the special case when we are dealing with mechanical systems these equations are called Lagrange’s equations.