Upon division of one integer with another, we obtain a quotient and a remainder. We have for instance that
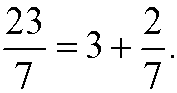
This expression can be rewritten as
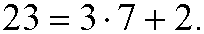
Both those expressions should be interpreted as if we divide 23 with 7, we get the quotient 3 and the remainder 2. Generally speaking, we have the following theorem:
Theorem: (Division algorithm) For every integer a (called dividend) and every integer b<>0 (called divisor), there is a unique integer q (called quotient) and a unique integer r (called remainder) such that
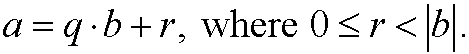
We use the division algorithm when we want to write a number in different bases. We normally use the base 10 (decimal number system) by tradition, probably because the ancient way of counting with fingers. The number 56342 should be interpreted as two ones, 4 tens, 3 hundreds, 6 thousands and 5 ten thousands added together, that is
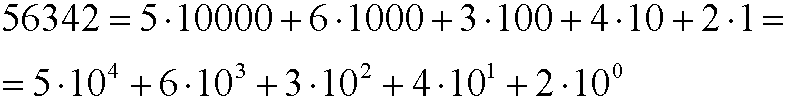
In computer science, one often works with (digital) components that only may attain two different states: on or off. It is then natural to use the number 2 as base, the so called binary number system. Here we only need two digits, 0 eller 1. We thus need to be able to convert numbers given in the decimal and binary number systems. The binary number 1101001 is converted to decimal form according to
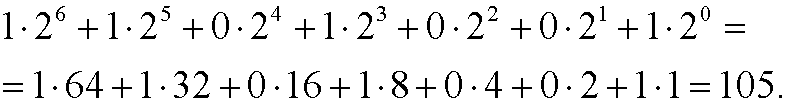
To be able to convert from decimal to binary we instead need to use the division algorithm. Let us find the binary representation of the decimal number 141. If we successively cut 141 into half, we get
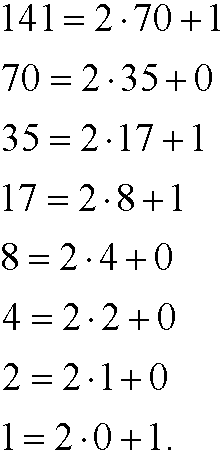
If we now put these steps together we get
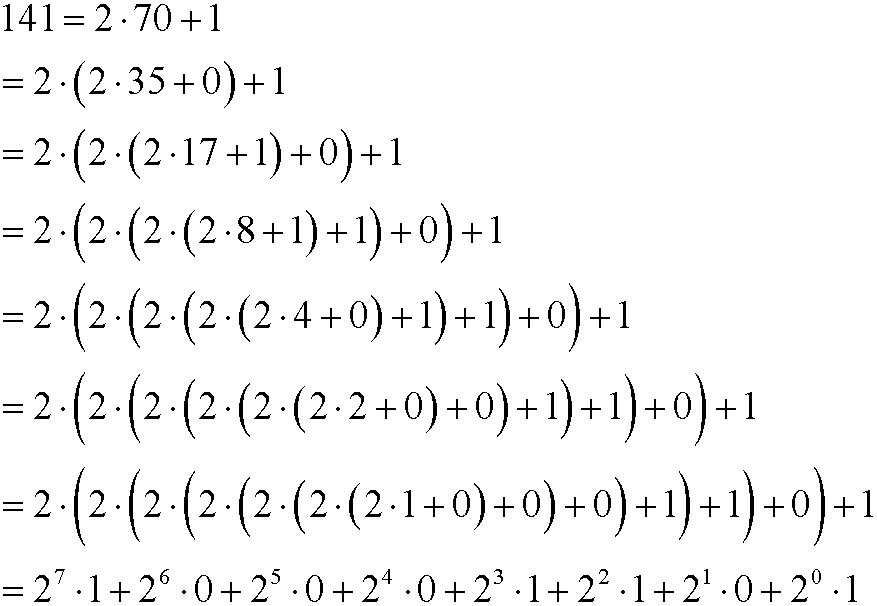
The decimal number 141 is thus written 10001101 binary, that is, the as the sequence of remainders we got from the division, read from down upwards. Binary numbers often get very long, therefore are often octal(base 8) or hexadecimal (base 16) numbers used instead. These two systems are used because they are very easy to convert back or forward to binary numbers. The same algorithm as above gives that
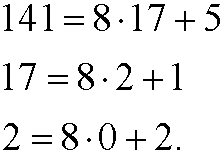
that is, 141 is written in the octal base as 215. We can achieve the same result by using that 23=8 and therefore group the binary number into groups of 3:
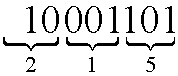
In the same way we do with hexadecimal numbers. Since we in this case need 16 digits, we need to introduce new symbols in addition to 0-9 for the “digits” 10-15. We use A for 10, B for 11, C for 12, D for 13, E for 14 and F for 15. We then get that
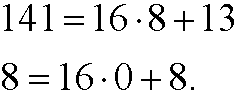
or
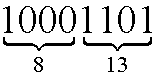
The decimal number 141 is thus written 8D in the hexadecimal base.