We will here derive the heat equation we used in the previous part. We start by stating a conservation law of the type “increase of quantity in the region = flow in to the region – flow out of the region”. In this case we imagine heat flowing along a long slender metal rod with cross section A. Let q(x,t) denote the amount of heat and j(x,t) denote the heat flow per unit time and unit area in the point x at time t.
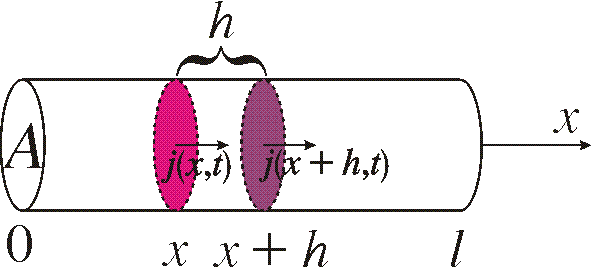
Let h be a small displacement in x. No consider the volume that corresponds to the interval [x,x+h]. The increase of quantity per unit time in this volume, that is, the time derivative of the amount q(x,t), is according to the conservation law above equal to the amount that flows in through the cross section at x minus the amount that flows out through the cross section at x+h, that is
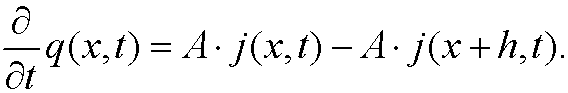
We know from thermodynamics that the amount of heat q(x,t) is
where c is the heat capacity of the material, m the mass of the region and u(x,t) the temperature. But the mass is the density multiplied with the volume of the region, that is
This means that we have the equation
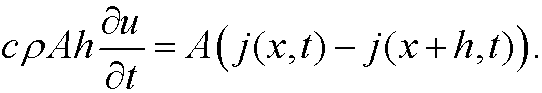
If we divide by Ah and let h go to zero, we get that
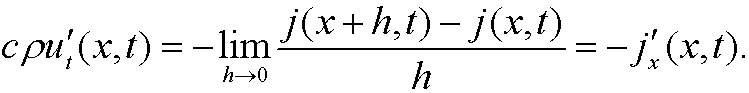
This is the continuity equation for heat flow. The heat flow j(x,t) is governed by Fourier’s law that statess that the heat flow is proportional to the heat change per unit length and takes place in the direction the heat decreases most, that is
where 
is the heat conductivity of the material. If we insert Fourier’s law into the continuity equation, we get
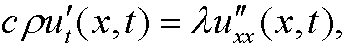
that is
where k is the so called heat diffusivity
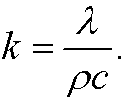
This is the one dimensional heat equation.