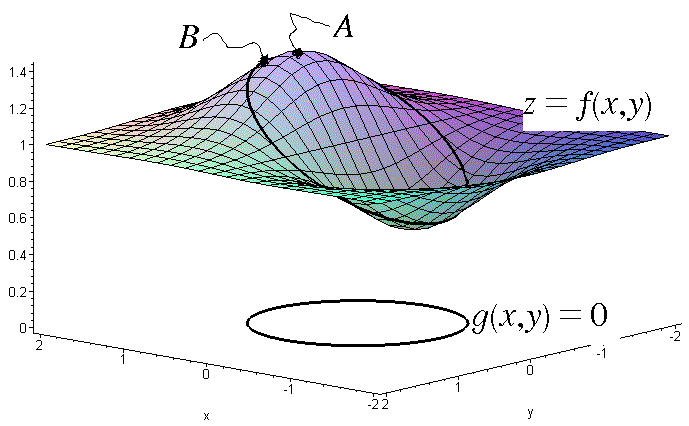
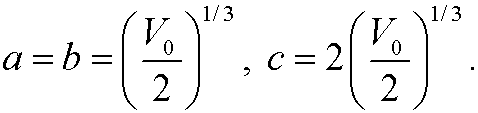In the figure below we have illustrated an extreme value problem with constraints. The point A is the largest value of the function z=f(x,y) while the point B is the largest value of the function under the constraintg(x,y)=0.
Theorem: (Lagrange multipliers) Let f and g be differntiable functions, where f’x(x0,y0) and f’y(x0,y0) not both are zero. If the function f(x,y) has an extreme value in the point (x0,y0) under the constraint g(x,y)=0, then there is a constant ![]() such that
such that
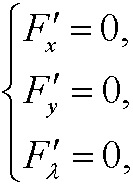
where
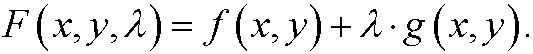
Remark: A similar theorem holds for a general function f(x1,x2,…,xn) with m constraints.
Example: The case n=3, m=2. Write the constraints as g1(x,y,z)=0 and g2(x,y,z)=0 and consider
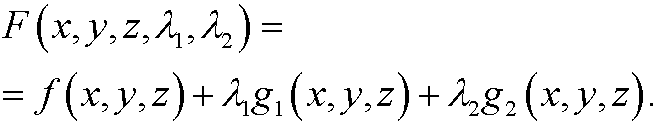
An (if existent) extreme value can be found by solving the system
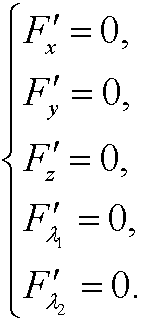
Example 6: How to construct a box with the same shape as in the figure below with a fix volume V0 such that the amount of material used will be minimal?
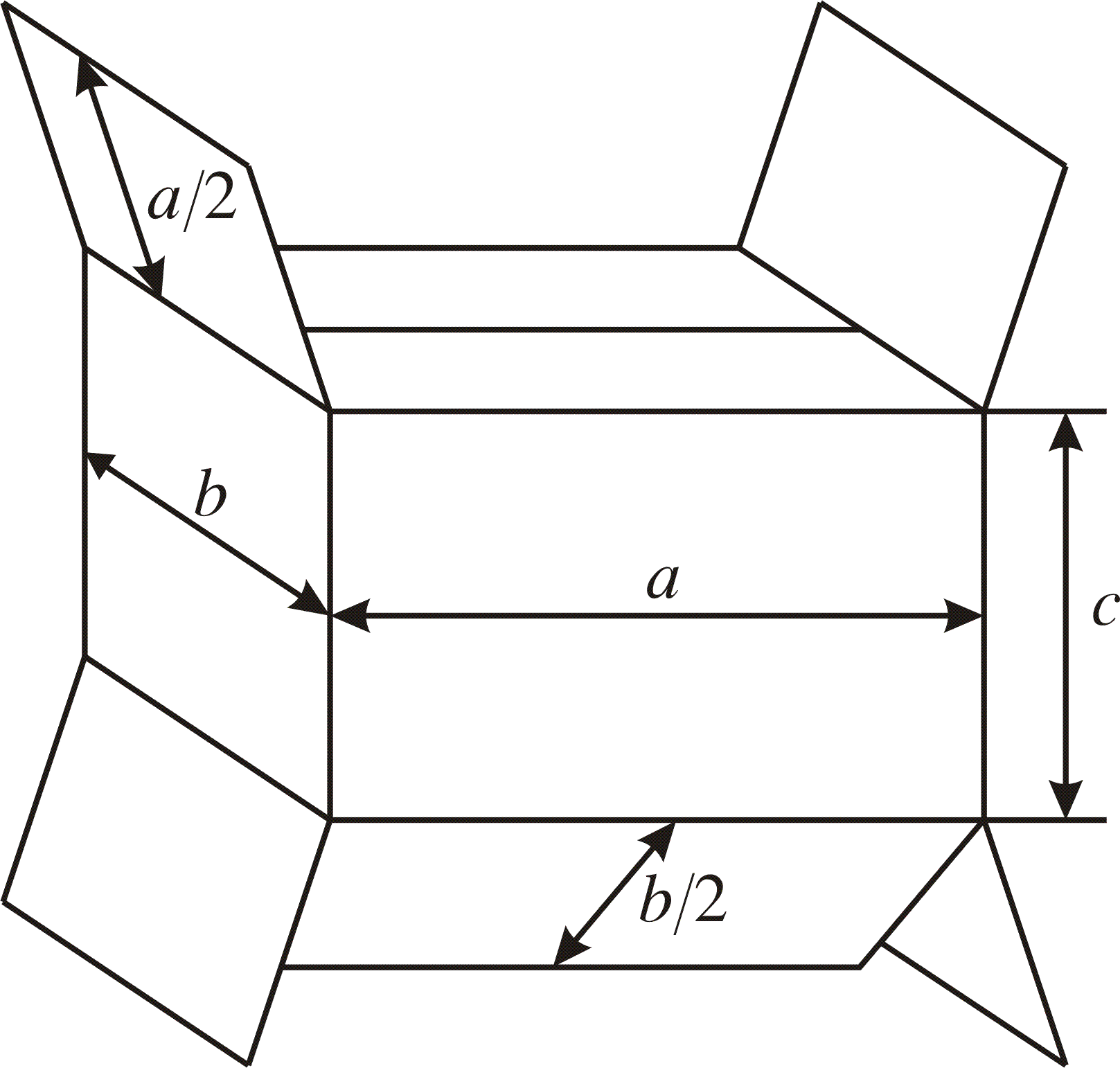
Solution: The problem consists of minimizing the amount of material (proportional to the area)
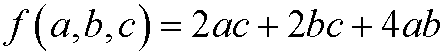
under the constraint
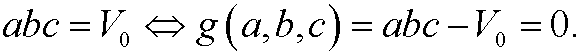
By Lagrange’s multiplier method we therefore construct
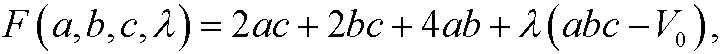
and then solve the system
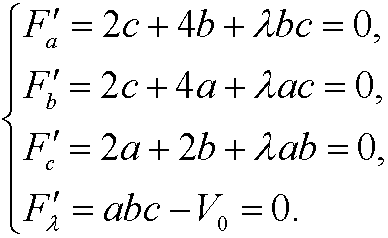
Multiply the first equation with a, the second with b and the third with c. By using that abc=V0, we get
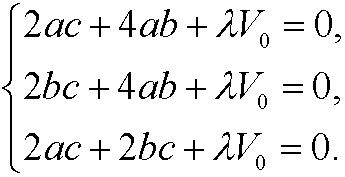
If we subtract the second equation from the first we get
since a,b,c>0. If we then put a=b in the last two equations we get
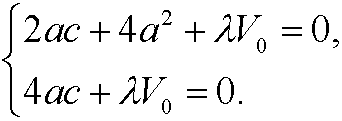
Now subtract the second of these two equations from the first
We should thus choose
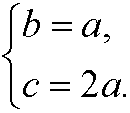
Inserted in the expression for the volumen we then have
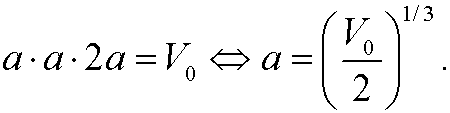
This imples that we should choose