Consider a physical law
made of m different quantities q1, q2,…,qm. These quantities have different dimensions which means that they can be expressed with help of a number of fundamental dimensions L1, L2,…,Ln, where n<m. In general, we can write the dimension of qi (denoted [qi]) as
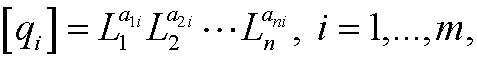
for some choice of exponents a1i,a2i,…,ani. If [qi]=1 we say that qi is dimensionless. The so called dimension matrix
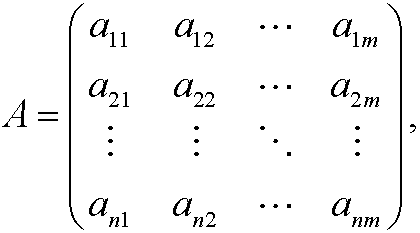
is a n*m matrix where the elements in the i:th column contains the exponents for qi in form of powers of L1,…,Ln. The fundamental assumption about the physical law is of the same type as the popular saying that you cannot compare apples and oranges. We say that the law is unit free in that sense that it is independent of the specific amount of units chosen to express the quantities q1, q2,…,qm. We differentiate between the words unit and dimension. With units we mean certain physical units as seconds, hours, days and years. On the other hand, all of these units have the dimension time. Every fundamental dimension Lj has the property that its units can be changed by multiplication by suitable factors
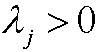
to obtain Lj in a new unit system. We write
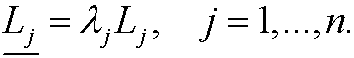
If q has the dimension
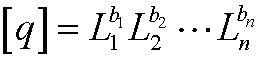
q is given by
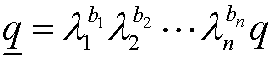
in the new unit system.