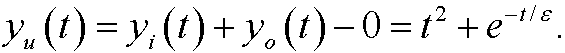Example: Consider the differential equation
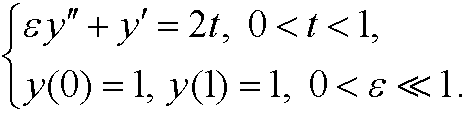
We get the outer approximation by putting 
and solving the equation with the outer boundary condition:
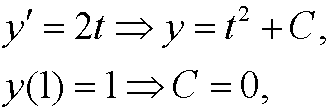
that is,
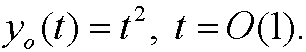
We now look for the inner approximation. Put
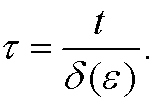
The equation is then transformed to
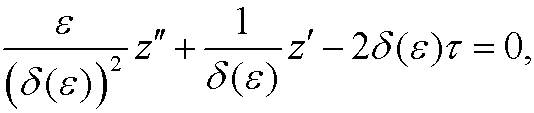
where
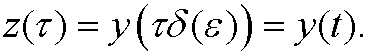
We compare the leading coefficient
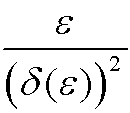
with the other (
is supposed to be small):
| Case1): |  |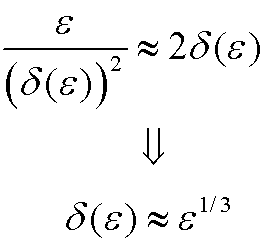
 |
 |
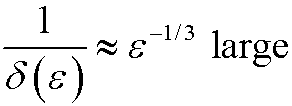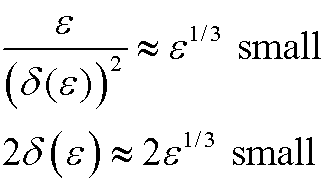| Case 2): |  |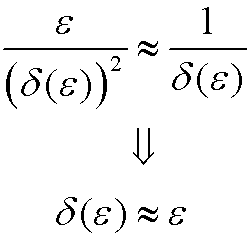
 |
 |
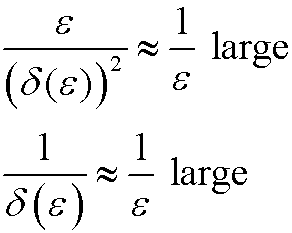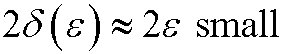We see that in Case 2, the remaining coefficient is much smaller than the other two. We therefore choose
and make the change of variables
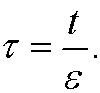
Our equation then becomes
We get the inner approximation when we put and solve the equation:
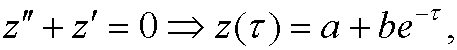
which in the original variables is
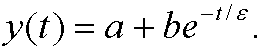
The condition y(0)=1 then gives
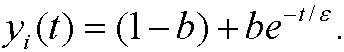
Let us match these approximations. Introduce the intermediate variable
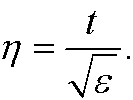
The matching condition
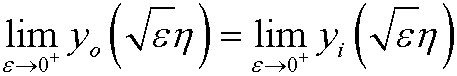
then implies that
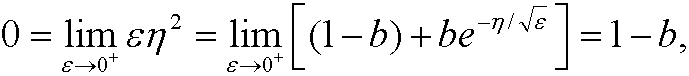
that is,
Our inner approximation finally becomes
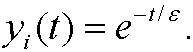
We get a unit approximation yu by adding the inner and outer approximations and subtracting their common limit in the overlapping region
