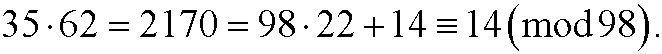Example 1: The time is now 21:00. Class will start in 11 hours. What will the time be then?
The answer to this question is not 21+11=32 but rather 21+11-24=8. When the time passes 23:59:59, we start over from zero again. The time on a watch is actually the remainder upon integer division by 24; we have that
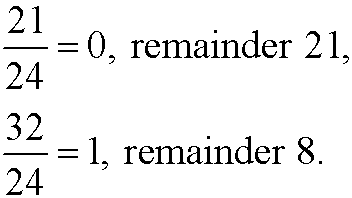
When you are only interested in the remainders and not care about the quotients, we talk about congruences. When we calculate with the remainders from division by the integer n, we say that we calculate modulo n or that we calculate in Zn. Two numbers with same remainder upon divison by the integer n are called congruent modulo n. We have for instance that
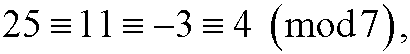
since
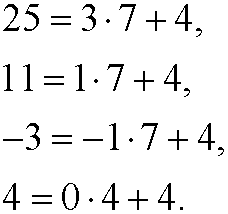
That the numbers 25, 11, -3 and 4 are congruent modulo n we can denote as that they belong to the equivalence class [4]7, called residue class 4 modulo 7. The residue classes modulo 7 are the sets
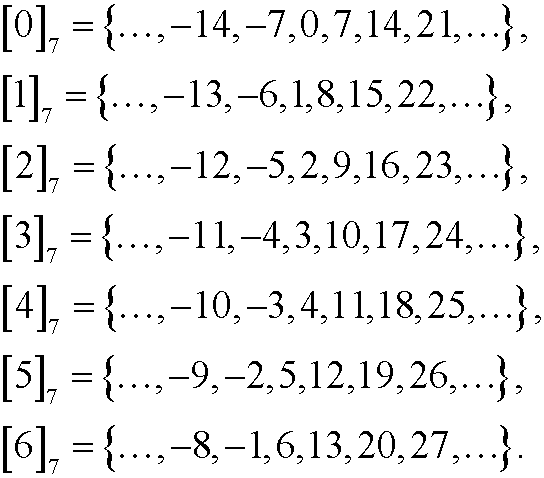
We see that the residue classes constitutes a partition of the set of all integers Z, since the residue classes are mutually disjoint as well as their union are equal to Z.
Example 2: Add 34 and 51 modulo 7. We can either compute the sum directly
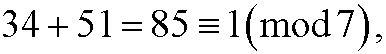
or stepwise
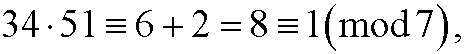
since 85=7*12+1, 34=7*4+6 and 51=7*7+2.
Example 3: Compute 34 multiplied by 51 modulo 7. We can either compute the product directly
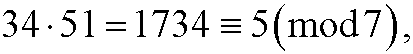
or stepwise
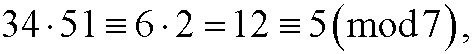
Example 4: Calculate the inverse to 3 modulo 7. The inverse to a number a is a number b=a-1 such that the product ab=1. Let us make a table over the products modulo 7 between the integers 0-6. We have
| * |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
| 2 |
0 |
2 |
4 |
6 |
1 |
3 |
5 |
| 3 |
0 |
3 |
6 |
2 |
5 |
1 |
4 |
| 4 |
0 |
4 |
1 |
5 |
2 |
6 |
3 |
| 5 |
0 |
5 |
3 |
1 |
6 |
4 |
2 |
| 6 |
0 |
6 |
5 |
4 |
3 |
2 |
1 |
We see from the table that 3-1 is 5, since
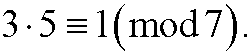
Example 5: Compute the inverse to 3 modulo 6. We construct a similar table as in the example above. We have
| * |
0 |
1 |
2 |
3 |
4 |
5 |
| 0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
1 |
2 |
3 |
4 |
5 |
| 2 |
0 |
2 |
4 |
0 |
2 |
4 |
| 3 |
0 |
3 |
0 |
3 |
0 |
3 |
| 4 |
0 |
4 |
2 |
0 |
4 |
2 |
| 5 |
0 |
5 |
4 |
3 |
2 |
1 |
In this case there is no inverse to 3 since there is no number that gives the product 1 (modulo 6) upon multiplication by 3.
Example 6: Solve the equation
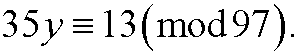
This is the same as saying that
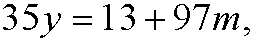
for some integer m. If we put m=-x we get the diophantine equation
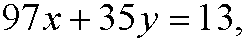
that we solved in example 1 in part 4. The solution of the diophantine equation is y=-468-97k, k integer. This means that the wanted solution is y=17, since there is only one solution y in the interval 0-96 (for k=-4), that is
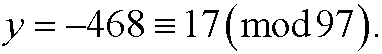
Example 7: Solve the equation
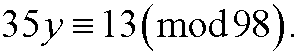
This is the same as saying that
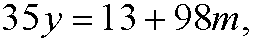
for some integer m. If we put m=-x we get the diophantine equation
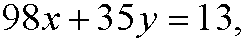
that had no solution in example 2 in part 4. This means that there is no solution to this equation.
Example 8: Solve the equation
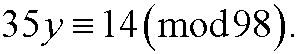
This is the same as saying that
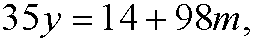
for some integer m. If we put m=-x we get the diophantine equation
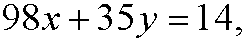
that we solved in example 1 i part 4. The solution of this diophantine equation is y=6-14k, k integer. This means that we have 7 solutions (as many as gcd(98,35)) in the interval 0-97. They are obtained fork=0,-1,-2,…,-6 and are
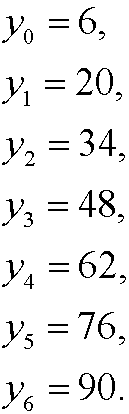
We can easily check that they are solutions by insertion in the equation. We have for instance that