Let z be a complex number and consider the function
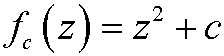
for a given parameter c. We choose a starting value z0 and investigate the orbit
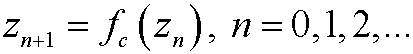
i) The case c=0. We have three choices:
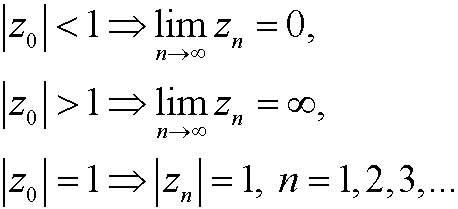
This is no fractal.
ii) The case ![]() . We now define the set Jc={z0: zn is inside a fix boundary in the plane}. This boundary is called a Julia set and is an example of a fractal.
. We now define the set Jc={z0: zn is inside a fix boundary in the plane}. This boundary is called a Julia set and is an example of a fractal.
For different starting points the orbits will either stay inside a bounded region or diverge to infinity. Those starting values that have bounded orbits are usually colored black while those diverging to infinity are colored in other colors depending on the speed with which they diverge. The results will be figures as those shown below. Note that the sets consists of the different starting values z0 for a given value of c. This implies that there are infinitely many different Julia sets.
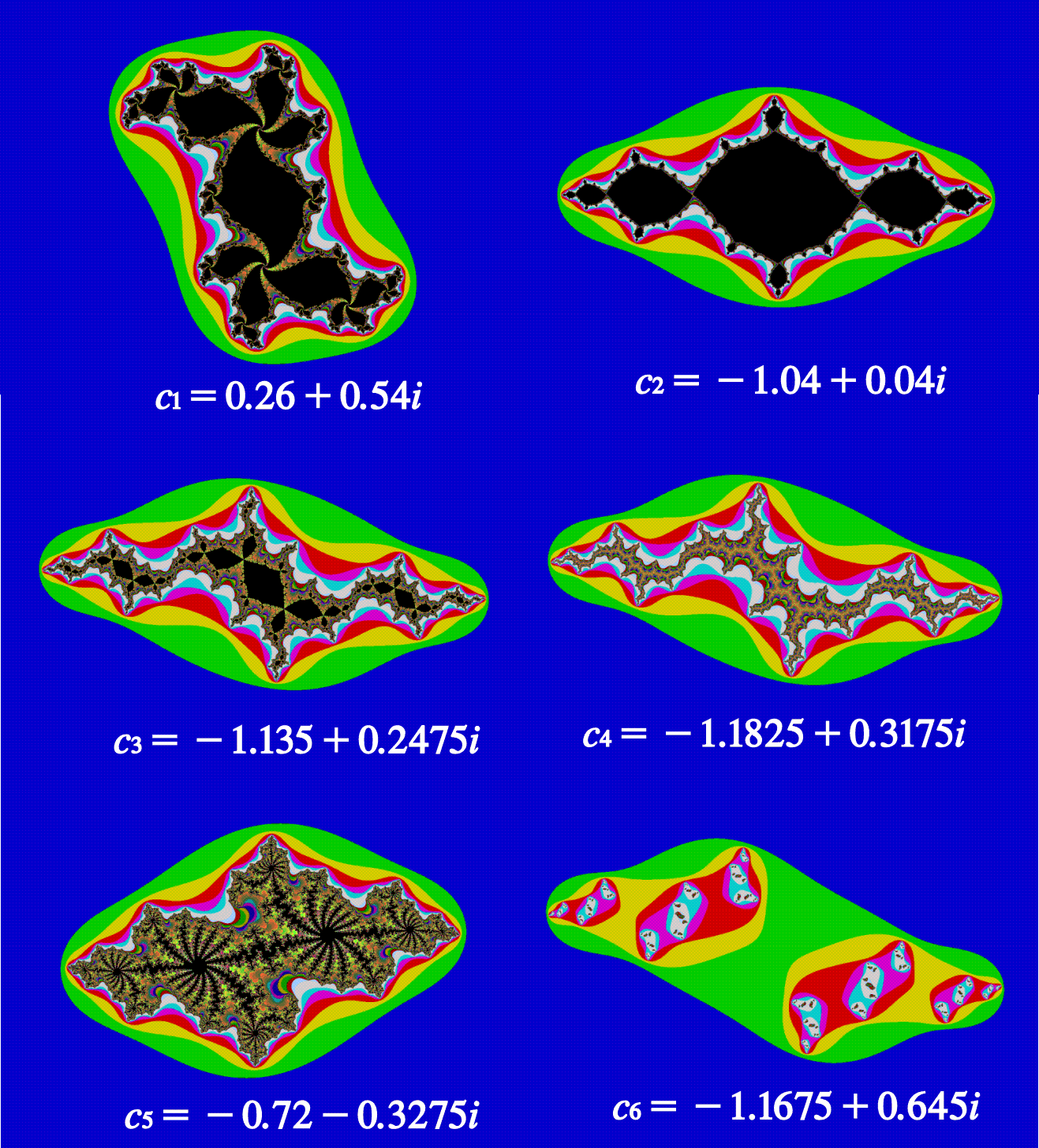
It can be shown that there is only two main types of Julia sets. Either the area inside boundary is connected or it is broken into infinitely many parts forming a cloud of points, with a fascinating fractal structure. The latter type is usually called a (general) Cantor set.
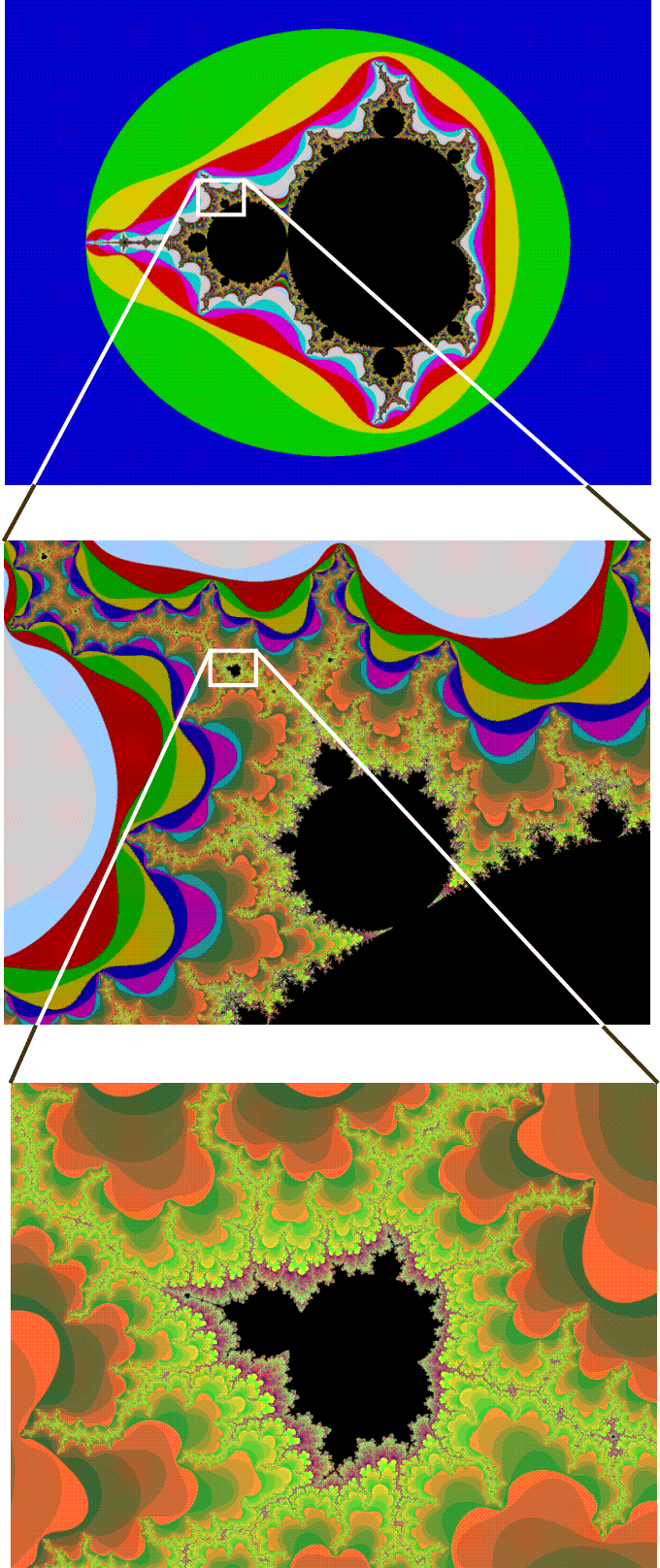
The Mandelbrot set is the set of all c such that the Julia sets are connected. This means that we can see the Mandelbrot set as a map over all Julia sets. The set is illustrated below with the values c for the above Julia sets.

Note that the Mandelbrot set is a set of values of c, in contrast to the Julia sets. The Mandelbrot set has a detailed structure on all scales. If we zoom in to look closer we see small copies of the Mandelbrot set everywhere. We also see that the set is everywhere connected. This self similar structure is typical for fractals. See the figure below.