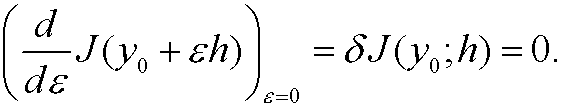14. A necessary condition for extremum of a functional.
Theorem 2: Let A be a subset of a normed linear space V and let
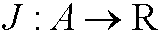be a given functional. if an element y0 in A gives a local minimum for J relative the norm ||.|| then
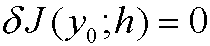for all admissible variations h.
Remark: The solutions to the problem above is called extremals.
Proof: Define the function
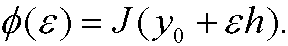This obviously a regular one-variable function
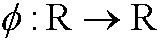and a necessary condition for extreme values to be attained in the point 
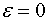is that
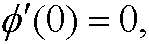that is,
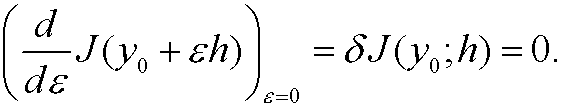The proof is complete.
