Consider the second order differential equation
![]()
where  is a small parameter,
is a small parameter,
![]()
We will try to solve it by inserting the perturbation series
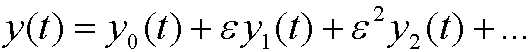
and then find y0(t), y1(t), y2(t),…
We can for instance use
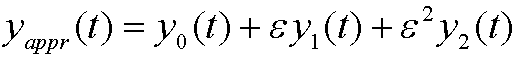
as a good approximation to the solution of the differential equation. Here y0(t) is the leading term, the solution of the unperturbed problem
The terms ![]() are higher order terms which usually are “small”.
are higher order terms which usually are “small”.
Remark: The unperturbed problem can in many cases be solved exactly.