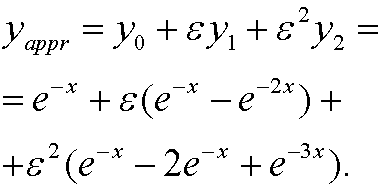Consider the equation form the last part
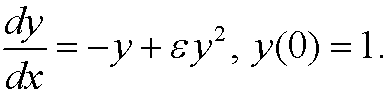
We expand y(x) in a perturbation series
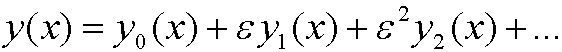
Insertion in the equation yields
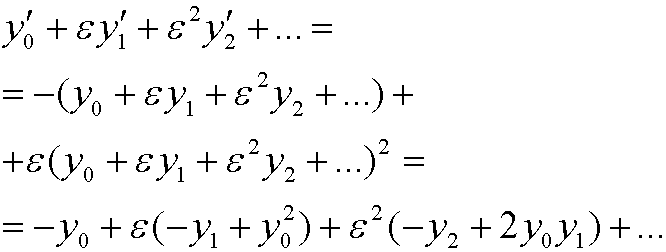
Insertion in the inital condition yields
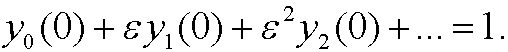
Now let
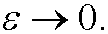
Then
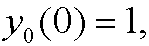
that is
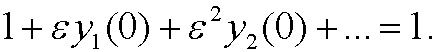
If we subtract 1 on both sides and divide the rest with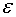 
we get
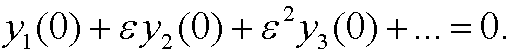
On more time, we let
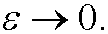
Then
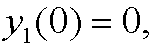
and if we repeat the procedure we realize that also
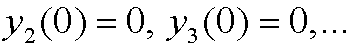
We determine y0, y1, y2,…. subsequently by solving the equations that we get by comparing terms containing the same power of :
 |
 |
 |
 |
 |
 |
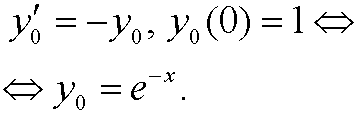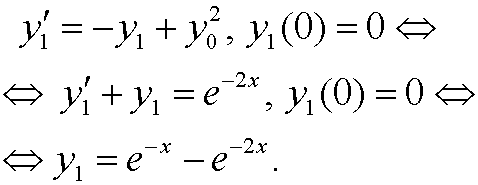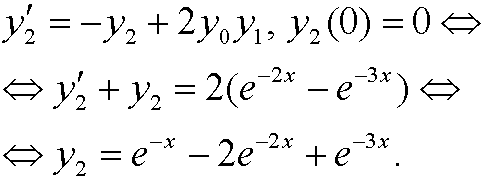An approximate solution is thus
