Theorem: Let
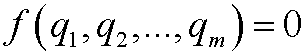
be a unit free physical law that relates the dimensioned quantities q1,q2,…,qm. Let L1,L2,…,Ln (where n<m) be the fundamental dimensions with
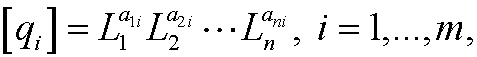
and let r=rank(A), where A is the dimension matrix. Then there are m-r independent dimensionless quantities
that can be formed from q1,q2,…,qm. Moreover, the physical law above is equivalent with an equation
which is solely expressed in dimensionless quantities.
Example: In our introductory example we had
(m=4) with the fundamental dimensions T, L, M (n=3) and
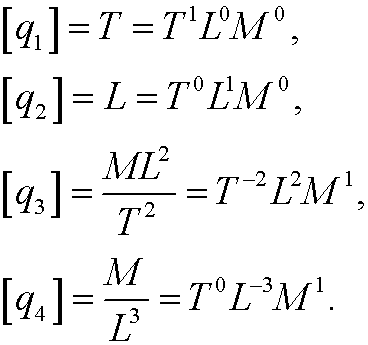
The dimension matrix will then become
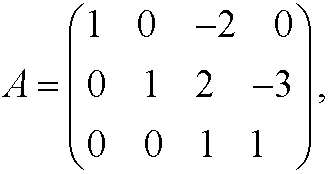
with rank(A)=3. This implies that we have m-r=4-3=1 dimensionless variable.
Remark: The following three characterisations of the rank rank(A) of a matrix A are equivalent:
1) The number of nonzero rows of the transformed upper triangular matrix.
2) The number of linearly independent rows or columns of A.
3) The highest order of nonzero subdeterminants to A.
Example: The matrix
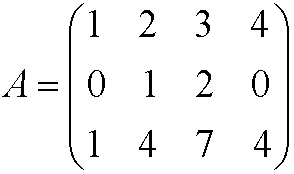
has rank 2.
Method 1 gives rank(A)=2 since admissible row operations show that
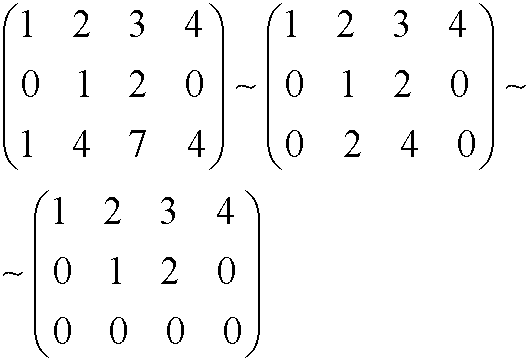
Method 2 gives rank(A)=2 since row3 is row1 plus 2 times row2 while row2 is not a multiple of row1.
Method 3 gives rank(A)=2 since
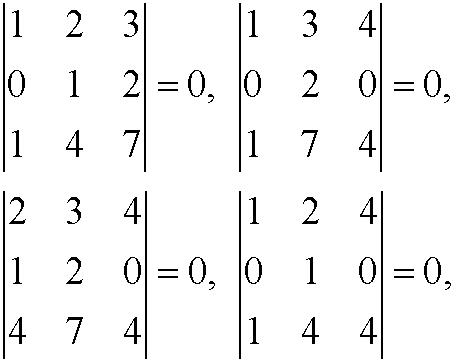
while
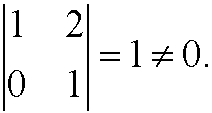
Proof (not complete) of the Pi-theorem:
Let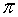 
be the dimensionless quantity
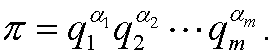
Expressed in the fundamental quantities L1,L2,,…,Ln we then have
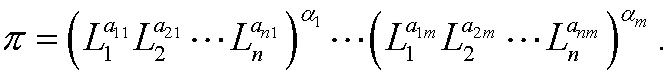
Since
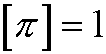
the exponents must be 0, that is
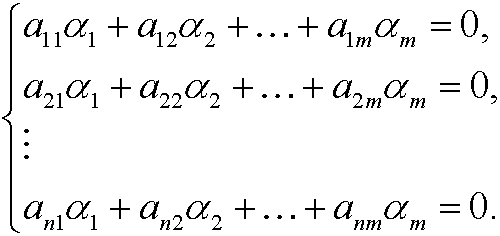
We have m unknowns and n equations, where m>n and the system rank is r. From linear algebra we know that there are m-r linearly independent solutions. Every such solution induces one dimensionless variable.