2.1) Consider the initial value problem
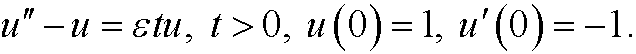
Find a two-term perturbation approximation u=u(t) for
2.2) Verify the following order relations:
a)
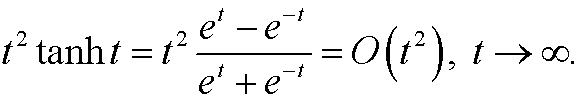
b)
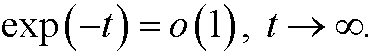
c)
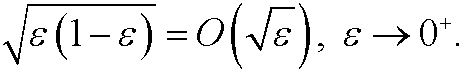
d)
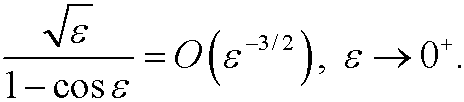
2.3) Use Poincaré-Lindstedt’s method to get a two-term perturbation approximation y=y(t) to the problem
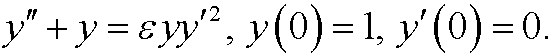
2.4) Consider the initial value problem
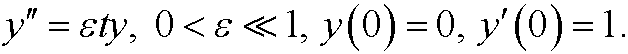
Use regular perturbation methods to achieve a three-term approximate solution y=y(t) for t>0.
2.5) Show that regular perturbation fails for the boundary value problem
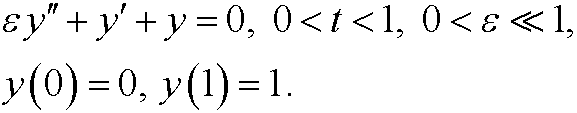
Find the exact solution y=y(t). If
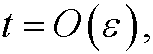
show that
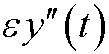
is large. If
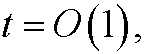
show that
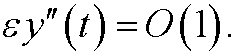
Find the inner and outer approxiamtions from the exact solution.
2.6) Suppose that
and use singular perturbation to find an approximate solution y=y(t) to the problem
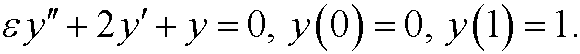
2.7) Show why singular perturbation fails for the boundary value problem
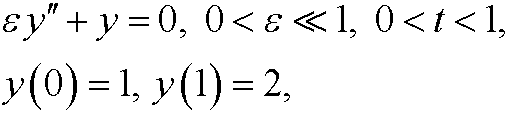
by comparing with the exact solution y=y(t).
2.8) Try singular perturbation on the boundary value problem
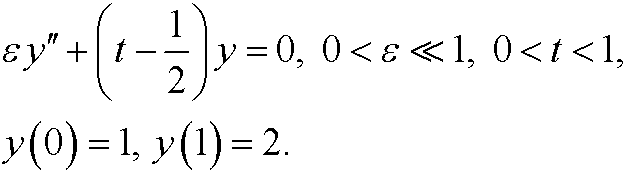
Discuss the result.